Теоретический закон распределения (TЗP) выражает общий характер изменения показателя надежности (ПН) машин и исключает частные отклонения, связанные с недостатками первичной информации. Процесс замены опытных закономерностей теоретическими называется в теории вероятностей процессом выравнивания (сглаживания) статистической информации.
В теории надежности для выравнивания опытной информации используют большое количество различных законов распределения. К таким законам, например, относятся: нормальный (Гаусса), экспонициальный, гамма-распределения, Вейбулла, Пуассона, Релля и др.
У каждого закона своя область применения, свои параметры и расчетные уравнения, свои заранее приготовленные таблицы, упрощения проведения расчетов. Каждый закон распределения показателей надёжности характеризуется двумя функциями:
§ дифференциальной функцией или функцией плотности вероятностей;
§ интегральной функцией распределения.
4.4.1 Выбор теоретического закона распределения
Применительно к показателям надежности автомобильной и тракторной техники используются в основном закон нормального распределения (3HP) и закон распределения Вейбулла (3PB). Предварительный выбор теоретического закона распределения (ТЗР) осуществляется по величине коэффициента вариации V. Если V < 0,3, то распределение подчиняется ЗНР, если V>0,5, –ЗРВ.
Если V лежит в интервале от 0,3 до 0,5, то выбирается тот закон, который лучше совпадает с опытной информацией; точность совпадения оценивается по критерию согласия.
В нашем случае коэффициент вариации V=0,48, поэтому подходят как ЗНР, так и ЗРВ. Для окончательного решения необходимо рассчитывать интегральную F(t) функцию распределения полного ресурса по ЗНР и ЗРВ, а затем с помощью критерия согласия выбирать TЗP.
4.4.2 Определение и построение интегральной функции для ЗНР
Значения интегральной функции F(t ki) в конце i-го интервала определяются по формуле
, (10)
где F0 – так называемая центрированная интегральная функции. Она табулирована и ее значение определяют по приложению Д;
– значение показателя надежности в конце i-го интервала статистического ряда (таблица 3);
– среднее значение показателя надежности;
σ – среднее квадратическое отклонение.
Необходимо помнить, что
F0(-t)=I-F(+t). (11)
4.4.3 Определение и построение интегральной функции для ЗРВ
Для ЗРВ значение интегральной функции F () в конце i-го интервала определяется по формуле
, (12)
где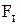 
– табулированное значение интегральной функции. Принимается по приложению Ж в зависимости от 
и параметра b;
с – сдвиг начала рассеивания. Для нашего примера С = 0;
а – параметр ЗРВ определяется по формуле
, (13)
где 
– коэффициент 3PB.
Параметр b и коэффициент определяется по приложению Е в зависимости от коэффициента вариации.
Полученные значения интегральных функций для 3HP и 3PB записывают в таблицу 4.
Тогда расчетное значение критерия согласия Колмогорова будет равно:
для ЗНР 
для ЗРВ 
Из приложения И находим вероятность совпадения теоретических законов с опытным распределением:
для ЗНР Р(λ) = 0,644,
для 3PB Р(λ) = 0,915.
Следовательно, для выравнивания опытной информации ЗРВ подходит лучше, чем 3HP. Выбрав окончательно в качестве теоретического закон ЗРВ, наносим на график интервалы и соединяем полученные точки плавной кривой, которая будет теоретической интегральной функцией распределения полного ресурса двигателя в соответствии с рисунком 2.
Таблица 4 - Выбор теоретического закона распределения
| Интервал, тыс. мото-ч | 0,9- 2,4 | 2,4- 3,9 | 3,9- 5,4 | 5,4- 6,9 | 6,9- 8,4 | 8,4- 9,9 | |
| Конец интервала,
| 2,4 | 3,9 | 5,4 | 6,9 | 8,4 | 9,9 | |
Накопленная вероят-ность (опытная) 
| 0,125 | 0,531 | 0,719 | 0,875 | 0,906 | 1,0 | |
| ЗНР | ( – )/σ
| -0,95 | -0,24 | 0,46 | 1,16 | 1,87 | 2,57 |
| F()
| 0,17 | 0,40 | 0,68 | 0,88 | 0,97 | 1,0 | |
| │ -F()│
| 0,045 | 0,131 | 0,039 | 0,005 | 0,064 | ||
| ЗРВ | ( –с)/а
| 0,48 | 0,78 | 1,09 | 1,39 | 1,69 | 1,99 |
| F()
| 0,18 | 0,43 | 0,70 | 0,87 | 0,96 | 0,99 | |
| │ -F()│
| 0,055 | 0,101 | 0,019 | 0,005 | 0,054 | 0,01 |
