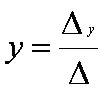Имеются данные по 30 территориям России
| Признак | Среднее значение | Среднее квадратическое отклонение | Парный коэффициент корреляции |
| у | 433,5 | 61,44 | 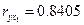
|
| х1 | 254,9 | 25,86 | 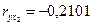
|
| х2 | 33,5 | 0,58 | 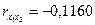
|
1. Построить уравнение множественной линейной регрессии в стандартизованном масштабе и в естественной форме.
Линейное уравнение множественной регрессии у от х1 и х2 имеет вид:  . Для расчета его параметров применим метод стандартизации переменных и построим искомое уравнение в стандартизованном масштабе:
. Для расчета его параметров применим метод стандартизации переменных и построим искомое уравнение в стандартизованном масштабе: 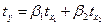 . Расчет β – коэффициентов выполним по формулам
. Расчет β – коэффициентов выполним по формулам
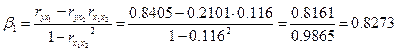
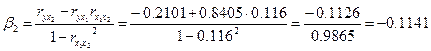 .
.
Получим уравнение 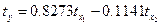 .
.
Для построения уравнения в естественной форме рассчитаем 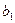 и
и 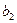 , используя формулы для перехода от β i к
, используя формулы для перехода от β i к 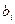 :
:
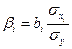 ;
; 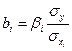 ;
;
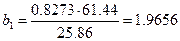 ;
; 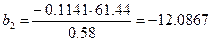 .
.
Значение a определим из соотношения
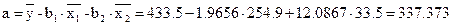
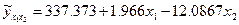
2. Рассчитайте частные коэффициенты эластичности.
Рассчитаем средние коэффициенты эластичности для определения относительной силы влияния х1 и х2 на у:

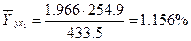 ;
; 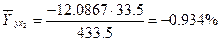 .
.
С увеличением средней заработной платы х1 на 1% от ее среднего уровня средний душевой доход у возрастет на 1,16 % от своего среднего уровня; при повышении среднего возраста безработного х2 на 1 % среднедушевой доход у снижается на 0,93 % от своего среднего уровня. Очевидно, что сила влияния средней заработной платы х1 на средний душевой доход у оказалась большей, чем сила влияния среднего возраста безработного х2. К аналогичным выводам о силе связи приходим при сравнении модулей значений β1 и β2.
3. Рассчитать линейные коэффициенты частной корреляции и коэффициент множественной корреляции.
Линейные коэффициенты частной корреляции здесь рассчитываются по рекуррентной формуле:
 ;
;
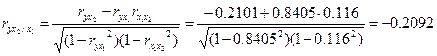 .
.
При сравнении значений коэффициентов парной и частной корреляции приходим к выводу, что из-за слабой межфакторной связи ( ) коэффициенты парной и частной корреляции отличаются незначительно: выводы о тесноте и направлении связи на основе коэффициентов парной и частной корреляции совпадают:
) коэффициенты парной и частной корреляции отличаются незначительно: выводы о тесноте и направлении связи на основе коэффициентов парной и частной корреляции совпадают:

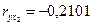 ;
;  ;
;
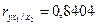 ;
; 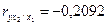 ;
;  .
.
Расчет линейного коэффициента множественной корреляции выполним с использованием коэффициентов 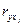 и β i:
и β i:
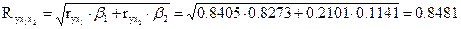
Зависимость у от х1 и х2 характеризуется как тесная, в которой 72 % вариации среднего душевого дохода определяются вариацией учтенных в модели факторов: средней заработной платы и среднего возраста безработного. Прочие факторы, не включенные в модель, составляют соответственно 28 % от общей вариации у.
4. Оцените значимость уравнения регрессии в целом с помощью F – критерия Фишера.
Общий F – критерий проверяет гипотезу Н0 о статистической значимости уравнения регрессии и показателя тесноты связи (R2=0):
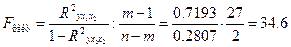 ;
;
 .
.
Сравнивая 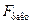 и
и 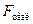 , приходим к выводу о необходимости отклонить гипотезу Н0, т.к.
, приходим к выводу о необходимости отклонить гипотезу Н0, т.к. 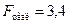 <
<  . С вероятностью 1-α=0,95 делаем заключение о статистической значимости уравнения в целом и показателя тесноты связи
. С вероятностью 1-α=0,95 делаем заключение о статистической значимости уравнения в целом и показателя тесноты связи 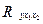 , которые сформировались под неслучайным воздействием факторов х1 и х2.
, которые сформировались под неслучайным воздействием факторов х1 и х2.
Приложение 4
Вопросы к зачету
1. Определение и предмет эконометрики.
2. Предмет и задачи эконометрики.
3. Спецификация парной линейной регрессии.
4. Метод выбора парной линейной регрессии.
5. Метод наименьших квадратов для построения парной модели.
6. Предпосылки метода наименьших квадратов.
7. Линейный коэффициент корреляции. Коэффициент детерминации.
8. Оценка существенности уравнения парной линейной регрессии.
9. Оценка существенности параметров линейной корреляции.
10. Проверка качества коэффициента корреляции.
11. Интервалы прогноза по линейному уравнению регрессии.
12. Средняя ошибка аппроксимации.
13. Классификация нелинейной регрессии. Гиперболическая модель.
14. Классификация нелинейной регрессии. Степенная модель.
15. Классификация нелинейной регрессии. Показательная модель.
16. Спецификация множественной линейной регрессии.
17. Отбор факторов при построении множественной регрессии.
18. Методы построения множественной линейной регрессии.
19. Выбор вида множественной линейной регрессии.
20. Оценка параметров уравнения множественной регрессии.
21. Частные коэффициенты корреляции.
22. Множественный коэффициент корреляции.
23. Коэффициент корреляции для нелинейной регрессии.
24. Оценка существенности результатов множественной регрессии и корреляции.
Пример 6.
Решите систему уравнений 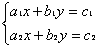
Решение
Для решения этой систему применим метод определителей.
Составим три определителя системы.
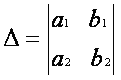
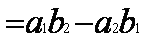
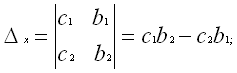
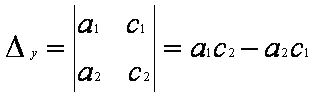
Теорема Крамера.
- Для того чтобы система имела единственное решение, необходимо и достаточно, чтобы главный определитель системы D был отличен от нуля. В этом случае решение системы находится по формулам:
 ;
;