1. Рассчитать параметры следующих функций:
- степенной;
- равносторонней гиперболы;
- показательной.
2. Найти показатели тесноты связи по каждой модели.
3. Оценить каждую модель через показатель детерминации, F – критерий Фишера, ошибку аппроксимации и выбрать наилучшую из них.
Регрессия в виде степенной функции имеет вид: 
.
Для оценки параметров модели линеаризуем модель путем логарифмирования:
.
Обозначим 
. Тогда получим: 
. Для расчетов составим таблицу 3.
Таблица 3.
| Номер региона | X | Y | ХY | 
| 
| 
| 
| 
| 
|
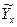
| 1,504 | 4,231 | 6,364 | 2,262 | 17,901 | 4,228 | 68,6 | 0,04 | 0,29 | |
| 1,775 | 4,066 | 7,217 | 3,151 | 16,532 | 4,071 | 58,6 | 0,09 | 0,51 | |
| 1,740 | 4,137 | 7,198 | 3,029 | 17,115 | 4,092 | 59,9 | 7,29 | 4,31 | |
| 1,974 | 3,953 | 7,803 | 3,897 | 15,626 | 3,957 | 52,3 | 0,04 | 0,38 | |
| 1,825 | 3,948 | 7,296 | 3,329 | 15,984 | 4,042 | 56,9 | 5,76 | 4,40 | |
| 1,792 | 4,045 | 7,249 | 3,211 | 16,362 | 4,062 | 58,1 | 1,00 | 1,75 | |
| 2,054 | 3,932 | 8,076 | 4,219 | 15,461 | 3,910 | 49,9 | 1,21 | 2,16 | |
| Сумма | 12,664 | 28,362 | 51,203 | 23,098 | 114,98 | 28,362 | 404,3 | 15,43 | 13,80 |
| Среднее значение | 1,809 | 4,052 | 7,315 | 3,300 | 16,426 | - | - | - | - |
Запишем систему нормальных уравнений:
.
Отсюда 
, 
; 
, 
Получаем уравнение регрессии: 
.
Выполнив потенцирование, получим:
.
Параметр 
означает коэффициент эластичности, который показывает, что с ростом зарплаты на 1 % доля расходов на продовольствие снижается на 0,58 %.
Теоретические значения зависимой переменной получим, подставив в уравнение значения х и потенцируя значения 
. В таблице 3. представлены 
и .
Показателем тесноты связи выступает индекс корреляции:
.
Величина 
представлена в таблице 3: 
.
.
В результате имеем:
.
Коэффициент детерминации равен: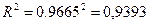 
, т.е. 93,93 % вариации у объясняется вариацией х, на долю прочих факторов приходится 6,07 %.
F – критерий Фишера составит:
.
Эта величина превышает табличное значение на 5 %-м уровне значимости (Fтабл=6,61). Следовательно, найденное уравнение регрессии 
статистически значимо.
Для расчета средней ошибки аппроксимации воспользуемся последней графой таблицы 3.
т.е. среднее отклонение фактических и расчетных значений у составляет 2 %, что свидетельствует о хорошем качестве модели.
Регрессия в виде показательной функции имеет вид: 
.
Для оценки параметров модели линеаризуем модель путем логарифмирования:
.
Обозначим 
. Тогда получим: 
. Для расчетов составим таблицу 4.
Таблица 4.
| Номер региона | х | Y | xY | 
|
|
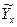
| y-
| (y- )2
| (y-  )2
|
|
| 4,5 | 4,23 | 19,04 | 20,25 | 4,21 | 67,35 | 1,45 | 2,11 | 121,63 | 2,111464 | |
| 5,9 | 4,07 | 23,99 | 34,81 | 4,08 | 59,06 | -0,76 | 0,57 | 0,28 | 1,296827 | |
| 5,7 | 4,14 | 23,58 | 32,49 | 4,10 | 60,17 | 2,43 | 5,88 | 23,32 | 3,873993 | |
| 7,2 | 3,95 | 28,46 | 51,84 | 3,96 | 52,27 | -0,17 | 0,03 | 32,17 | 0,33356 | |
| 6,2 | 4,00 | 24,79 | 38,44 | 4,05 | 57,42 | -2,92 | 8,51 | 10,70 | 5,351722 | |
| 4,04 | 24,27 | 4,07 | 58,50 | -1,40 | 1,97 | 0,45 | 2,459651 | |||
| 7,8 | 3,93 | 30,67 | 60,84 | 3,90 | 49,41 | 1,59 | 2,52 | 45,85 | 3,113949 | |
| Сумма | 43,3 | 28,36 | 174,80 | 274,67 | 28,36 | 404,19 | 21,60 | 234,39 | 18,54 | |
| Средняя | 6,19 | 4,05 | 24,97 | 39,24 |
Запишем систему нормальных уравнений:
.
В результате: 
Получаем уравнение регрессии: 
. Теперь потенцируем оба параметра, чтобы получить уравнение регрессии в форме показательной кривой:
.
Теоретические значения зависимой переменной получим, подставив в уравнение значения х и потенцируя значения . В таблице 4. представлены и .
Показателем тесноты связи выступает индекс корреляции:
.
Величина представлена в таблице 4: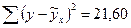 
.
.
В результате имеем:
.
Коэффициент детерминации равен: 
, т.е. 90,24 % вариации у объясняется вариацией х, на долю прочих факторов приходится 9,76 %.
F – критерий Фишера составит:
.
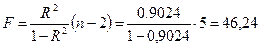Эта величина превышает табличное значение на 5 %-м уровне значимости (Fтабл=6,61). Следовательно, найденное уравнение регрессии статистически значимо.
Для расчета средней ошибки аппроксимации воспользуемся последней графой таблицы 4.
т.е. соответствие фактических и расчетных значений зависимой переменной хорошее и соответственно хорошее качество модели.
Регрессия в виде равносторонней гиперболы имеет вид: 
.
Чтобы оценить параметры уравнения приведем модель к линейному виду, заменив 
. Тогда 
. Применяя МНК, получаем систему нормальных уравнений:
Для расчета параметров составим таблицу 5.
Таблица 5.
| Номер региона | у |
| yz | 
| 
| 
|
|
|
| 68,8 | 0,222 | 15,289 | 0,049 | 69,9 | -1,1 | 1,21 | 1,60 | |
| 58,3 | 0,170 | 9,881 | 0,029 | 58,5 | -0,2 | 0,04 | 0,34 | |
| 62,6 | 0,175 | 10,983 | 0,031 | 59,8 | 2,8 | 7,84 | 4,47 | |
| 52,1 | 0,139 | 7,236 | 0,019 | 51,9 | 0,1 | 0,01 | 0,19 | |
| 54,5 | 0,161 | 8,790 | 0,026 | 56,7 | -2,2 | 4,84 | 4,04 | |
| 57,1 | 0,167 | 9,517 | 0,028 | 57,9 | -0,8 | 0,64 | 1,40 | |
| 51,0 | 0,128 | 6,538 | 0,016 | 49,6 | 1,4 | 1,96 | 2,75 | |
| Сумма | 404,4 | 1,162 | 68,234 | 0,198 | 404,4 | 16,54 | 14,79 |
Запишем систему нормальных уравнений:
.
Отсюда 
, 
; 
, 
Получаем уравнение регрессии: 
.
Показателем тесноты связи выступает индекс корреляции:
.
Величина представлена в таблице 5: 
.
.
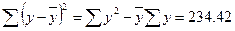В результате имеем:
.
Коэффициент детерминации равен: 
, т.е. 92,94 % вариации у объясняется вариацией х, на долю прочих факторов приходится 7,06 %.
F – критерий Фишера составит:
.
Эта величина превышает табличное значение на 5 %-м уровне значимости (Fтабл=6,61). Следовательно, найденное уравнение регрессии статистически значимо.
Для расчета средней ошибки аппроксимации воспользуемся последней графой таблицы 5.
т.е. среднее отклонение фактических и расчетных значений у составляет 2 %, что свидетельствует о хорошем качестве модели.
Выберем наилучшую модель, для чего объединим результаты построения парных регрессий в одну таблицу.
Таблица 6. - Сводная таблица построенных уравнений
| Уравнение регрессии | Коэффициент детерминации | F – критерий Фишера | Средняя ошибка аппроксимации, % |
|
| 0,9393 | 77,4 | 1,97 |
|
| 0,9024 | 46,24 | 2,65 |
|
| 0,9294 | 65,8 | 2,11 |
Все уравнения регрессии достаточно хорошо описывают исходные данные. Некоторое предпочтение можно отдать степенной функции, для которой значение коэффициента детерминации наибольшее, а ошибка аппроксимации – наименьшая.
