1. Четвертый и шестой члены арифметической прогрессии равны
соответственно 2 и 6. Найти третий член прогрессии.
1). 2; 2). - 2; 3). 0; 4). 0,5.
2. Числа 3 и 5 являются соответственно третьим и седьмым членами
арифметической прогрессии. Найти второй член прогрессии.
1). 2,5; 2). 1,5; 3). 2; 4). 0,5.
3. В арифметической прогрессии найти а 13, если а 1 = 7, d = 4.
1). 48; 2). 55; 3). 62; 4). 5,5.
4. В арифметической прогрессии а 1 = 14,5, разность прогрессии d = 0,7.
Найдите номер п члена арифметической прогрессии, если ап равен 32.
1). -26; 2). 25,6; 3). 26; 4). 21/19.
5. Восьмой член арифметической прогрессии, члены которой 16; 10; 4; …,
равен
1). -14; 2). - 18; 3). -22; 4). – 26.
6. Сумма трех чисел, образующих возрастающую арифметическую прогрессию,
равна 0, а сумма квадратов этих чисел равна 8. Найти сумму четвертых степеней
этих чисел.
1). -32; 2). 32; 3). 23; 4).0..
7. Найдите девятнадцатый член арифметической прогрессии, если известно, что
ее девятый член равен (- 40), а разность прогрессии равна 3
1). 20; 2). - 10; 3). 12; 4). 10.
8. Найдите сумму первого члена и разности арифметической прогрессии, в
которой:
1). - 4; 2). 4; 3).– 2; 4). 2.
9. Найдите возрастающую арифметическую прогрессию, у которой сумма
первых трех членов равна 27, а сумма их квадратов равна 275.
1). - 5; - 9; - 13; - 17;… 2). 5; 9; 13; … 3). 9;5;1;- 3;… 3). 
10. В арифметической прогрессии сумма второго и пятого членов равна 8, а
третьего и седьмого равна 14. Найдите сумму четвертого и шестого членов.
1). – 18; 2). 14; 3). – 14; 4). 16.
11. От деления шестнадцатого члена арифметической прогрессии на пятый в
частном получается 3, а от деления двадцать первого члена на шестой в частном
получается 3 и в остатке 12. Найдите сумму первых трех членов прогрессии.
1). 18; 2). 24; 3). 36; 4) 45.
12. Произведение третьего и шестого членов арифметической прогрессии равно
406. При делении девятого лена этой прогрессии на ее четвертый член в частном
получается 2, а в остатке 6. Найдите первый член и разность прогрессии.
1). 4 и 5; 2). – 5 и – 4; 3). – 10/7 и 16/7; 4) 10/7 и - 16/7;
13. В возрастающей арифметической прогрессии сумма первого и пятого членов
равна (- 4), а произведение второго и третьего членов равна 8. Найдите разность
этой прогрессии.
1). – 2; 2). 0,5 3). 2; 4). 1.
14. Сумма шестого и девятого членов арифметической прогрессии равна 20, а их
произведение равно 64. Найдите сумму пятого и десятого членов, если первый
член отрицательный.
1). – 20; 2) 20; 3). 52; 4). 64.
15. Найдите сумму первых четырех членов арифметической прогрессии, у
которой второй член равен 15, а третий равен 13.
1).42; 2). 80; 3). 56; 4). – 36.
16. Найдите сумму семи членов арифметической прогрессии, шестой член
которой равен 6, а сумма второго и пятого равна 3.
1).14,4; 2). 48; 3). 16,8; 4). 24.
17. Найдите сумму первых девяти членов арифметической прогрессии, у
которой третий член равен 13, а седьмой равен 1.
1). 73; 2) 88; 3). 63; 4). 56.
18. В арифметической прогрессии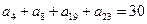 
. Найдите сумму
двадцати шести ее первых членов.
1). 171 2); 195 3). 215 4).225
19. Крайние члены арифметической прогрессии, имеющей 7 членов, равны 11 и
35. Сколько членов в другой арифметической прогрессии, крайние члены
которой 38 и 13, если четвертые члены обеих прогрессий одинаковые?
1). 8 2) 12; 3). 6 4). 24
20. Известно, что при любом п сумма 
членов некоторой арифметической
прогрессии выражается формулой = 5 п 2 – 4 п. Найдите три первых члена
этой прогрессии. В ответе укажите их произведение.
1). 32 2) 2 3). 14 4). 16
