1. (2 балла). Решите систему уравнений 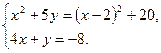
2. (4 балла). Среди всех значений х, удовлетворяющих первому неравенству
3 х 2 + 10 х + 3 ≥ 0, найдите все значения, не удовлетворяющие второму неравенству 3 х 2 + 10 х + 3 > 0.
3. (4 балла). В двух школах в начале учебного года было 1500 учащихся. К концу года число учащихся увеличилось в первой школе на 10 %, а во второй – на 20 %. В результате общее число учащихся стало равным 1720. Сколько учащихся стало в каждой школе к концу учебного года?
4. (6 баллов). Решите неравенство: 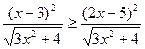 .
.
5. (6 баллов). График квадратичной функции проходит через точки А (4; 0); В (6; 0) и С (5; - 1). Задайте функцию формулой и постройте ее график.
Вариант 14.
Часть 1.
1. Укажите наибольшее из чисел:  ;
;  ;
;  ;
;  .
.
1)  2)
2)  3)
3)  4)
4) 
2. Среди учеников класса ровно одна треть девочек. Сколько процентов составляет количество мальчиков от количества девочек?
1) 50% 2) 20% 3) 70% 4) 200%
3. Найдите значение выражения 1 – 8х2 -15х3 при х = -  .
.
1)  2)
2)  3)
3)  4)
4)  .
.
4. Из формулы у =  выразите переменную с.
выразите переменную с.
1) с =  2) с = х -
2) с = х -  3) с = ух+ а 4) с =
3) с = ух+ а 4) с = 
5. Какая из следующих дробей тождественно равна дроби  ?
?
1)  2)
2)  3)
3) 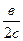 4)
4) 
6. Сократите дробь  .
.
Ответ _____________
7.Найдите значение выражения (1,5 · 10-3 )2.
1).2250000 2).0,0000000225 3). 0,00000225 4).2250000000
8. Одна из точек, отмеченных на координатной прямой, соответствует числу  Какая это точка?
Какая это точка?
О А В С
 | • | • | • | • |
| • | • | • | • |
6 7 8 9 10 х
1). В 2). А 3). С 4). О
9. Найдите сумму корней уравнения 3 х2 + 4х =0.
Ответ_________________
10.В классе количество девочек на 5 меньше количества мальчиков. Каждая девочка на празднование Нового года принесла 7 штук печенья, а каждый мальчик из общего количества принесенного печенья до празднования съел по 2 печенья, в результате чего к началу праздника осталось 40 штук. Пусть в классе х мальчиков и у девочек. Какая система уравнений соответствует условию задачи?
1)  2).
2).  3)
3)  4).
4). 
11 О положительных числах а, в и с известно, что с – а >0 и в – с > 0. Какое из следующих неравенств неверно?
1).  2).
2).  >
>  , 3). в – с > а – с, 4). –в < - а
, 3). в – с > а – с, 4). –в < - а
12. Решите неравенство 4 х2 
1). -0,5  2). -2
2). -2  3). х
3). х  4). х
4). х  .
.
13 На первой странице книги 1000 букв, а на каждой следующей на 10 меньше, чем на предыдущей. Сколько букв на странице с номером п?
1). 1010 -10 п 2). 990 – 10 п 3). 1000 – 10 п 4). 
14. Найдите корни уравнения 

15.График какой функции изображен на рисунке?
1). у = 2 - х; 2). у = 0,5 х – 13). у = 1 – 0,5 х 24). у = 5 х+ 2
|
|

Часть 2. Задания этой части выполняйте с записью решения
1. (2 балла) Упростите выражение  :
: 
2. (4балла) Решите уравнение 10 х 4 – 45 х = 30 х 2 – 15 х 3.
3. (4 балла) Постройте график функции у = х +  .
.
4. (6 баллов) В куске сплава меди и цинка количество меди увеличили на 40%, а количество цинка уменьшили на 40%. В результате общая масса куска сплава увеличилась на 20%. Определить процентное содержание меди и цинка в первоначальном куске сплава.
5. (6 баллов) Найдите все значения а, при которых точка пересечения прямых 3 х+ау+ 1= 0 и 2 х -3 у - 4 = 0 находятся в третьей координатной четверти.
Вариант 15.
Часть 1.
1.Расположите в порядке возрастания числа 6,99; 4 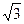 ;
;  .
.
Ответ ____________
2. В магазине произвели уценку товаров на 50%. Во сколько раз понизились цены в магазине?
Ответ_____________
3. Найдите значение выражения  при п = -3.
при п = -3.
Ответ________________
4.В 8кг сплава свинца и цинка содержится 3 кг свинца. Сколько цинка содержится в 5 кг такого же сплава?
Ответ__________________
5. Упростите выражение 
Ответ________________
6. Упростите выражение 

Ответ________________
7.Запишите число 0,000079 в стандартном виде.
1). 7,9 · 10-4; 2). 7,9 · 10-5 3). 7,9 · 10-6 4). 7,9· 10-7 .
8.Одна из точек на координатной прямой соответствует числу  Какая это точка?
Какая это точка?
О А В С М
 | • | • | • | • | • |
| • | • | • | • | • |
13 14 15 16 17 18 х
1). А 2). О 3 ). С 4 ). М 5 ). В
9. Найдите корни уравнения 
Ответ_________________
10. Одна из диагоналей параллелограмма больше другой диагонали на 5 см. Найдите длину меньшей диагонали, если их произведение равно 36.
Ответ_________________
11. Известно, что т < -1. Сравните числа т и  и укажите истинное из приведенных ниже утверждений:
и укажите истинное из приведенных ниже утверждений:
1). т >  ; 2). т <
; 2). т <  ; 3). т =
; 3). т =  ; 4).сравнить невозможно.
; 4).сравнить невозможно.
12. Решите неравенство (1-х) (х+4) > 0.
1).  2).
2). 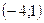 3)
3) 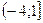 4).
4).  .
.
13. Решите систему уравнений 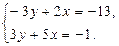
14.На первую клетку шахматной доски положили одно зерно, а на каждую следующую на 2 зерна больше, чем на предыдущую. Сколько зерен положили на последнюю клетку?
Ответ_______________
15. Найдите значение выражения: 
1).  ; 2).
; 2).  ; 3). – 7 -
; 3). – 7 - 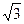 ; 4).
; 4).  .
.
16. Сестра старше брата на 6 лет, а через год будет старше его в 2 раза. Сколько лет сестре?
Ответ_______________
Часть 2. Задания этой части выполняйте с записью решения
1. (2 балла) Решите систему неравенств 

2. (4 балла). Найдите сумму всех трехзначных чисел, кратных 14.
3.(4 балла).Сплав золота с серебром, содержащий 80 г золота, сплавлен со 100 г чистого золота. В результате содержание золота в сплаве повысилось по сравнению с первоначальным на 20%. Сколько серебра в сплаве?
4 (6 баллов). Постройте график функции
 у =
у =  .
.
5 (6 баллов) Найдите все значения т, при которых парабола у = х2 – х+ 1 имеет с прямой х + ту -1= 0 одну единственную общую точку.
Вариант 16.
Часть1
1. Найдите значение выражения  при х = - 2.
при х = - 2.
1).  ; 2).
; 2).  ; 3). –6
; 3). –6  ; 4). – 14
; 4). – 14  .
.
2. Выразите из формулы площади трапеции Ѕ =  · h основание а.
· h основание а.
1). а =  ;
;  2). а =
2). а =  ; 3). a =
; 3). a = 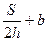 S;4). a =
S;4). a =  .
.
3. На первой странице книги 800 букв, а на каждой следующей на 10 меньше, чем на предыдущей. Сколько букв на странице с номером п?
1). 880 -10 п; 2). 790 – 10 п;3). 810 – 10 п;4).  .
.
4).Укажите точку, отмеченную на координатной прямой, соответствующую числу  .
.
|

11 12 13 14 15 16
1). Р 2). Х 3). Z 4 У.
5. Мотоциклист проходит расстояние АВ за 10,5час. На сколько процентов следует увеличить его скорость, чтобы то же расстояние он преодолел за 8 час 24 мин?
1).на 1%, 2). на 20%, 3). на 25%, 4). на 21%.
6.Какое из следующих выражений тождественно равно дроби  ?
?
1).  ; 2).
; 2).  ; 3).
; 3).  ; 4).
; 4).  .
.
7. Упростите выражение 4(а – b)2 – 4 b2.
1). 4 а2– 4аb, 2). 4 а2– 8 аb; 3). 4 а2– 5 b2; 4). 4 а 2– 4 b 2
8. Найдите значение выражения  .
.
1).5 2). 11 3). 3  4). 3
4). 3  .
.
9.Укажите наибольший корень уравнения 4 х 2 – 20 х = 0.
10.У причала находилось 6 лодок, часть из которых была двухместными, а часть трехместными. Всего в этих лодках может вместиться 14 человек. Сколько двуместных и сколько трехместных лодок было у причала?
Пусть у причала было х двуместных и у трехместных лодок. Какая система уравнений соответствует условию задачи?
1).  2).
2).  3).
3).  4).
4). 
11. Известно, что т 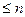 . Какое из следующих неравенств неверно?
. Какое из следующих неравенств неверно?
1).  ; 2). 9 т
; 2). 9 т 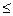 9 п; 3).–9 т
9 п; 3).–9 т 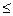 – 9 п; 4). т + 9
– 9 п; 4). т + 9 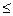 п + 9.
п + 9.
12. Решите неравенство  х2
х2  0,04.
0,04.
Ответ____________
13. Какое число не является членом арифметической прогрессии 4; 7; 10; 13;…?
1).31 2). 32 3). 34 4). 37
14.Используя графическое представление, подберите из данных уравнений второе уравнение системы 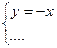 так, чтобы она не имела решений.
так, чтобы она не имела решений.
1) у = х2 2 ) у =  3) у = -
3) у = -  4). у = -3 –х2
4). у = -3 –х2
15.На координатной прямой отмечены числа а и b. Какое из нижеприведенных утверждений верно?
|
|
|
|





 1) а + b > b; 2). b – а > а;3 ) аb < b;4) b: а < а.
1) а + b > b; 2). b – а > а;3 ) аb < b;4) b: а < а.
16. Укажите рисунок, на котором приведена графическая иллюстрация решении системы уравнений 
|







