1. (2 балла). Упростите выражение: 
.
2. (4 балла) Найдите координаты точек пересечения графика функции
у = – х 3 – 2х2 + х + 2 с осями координат.
3. (4 балла). Упростите выражение 0,1(51-5 п )2(42 п +1)3 (2,5)11 п .
4. (6 баллов). Известно, что прямая, перпендикулярная прямой у = 0,125 х, касается параболы у = х2- 1. Вычислите координаты точки касания.
5. (6 баллов). Найдите множество значений параметра т, при которых число 2 находится между корнями уравнения 9 х2 – 6 х – (т – 2)(т +2)=0.
Вариант 12.
Часть1.
1. Найдите массу рельсов, составляющих полотно железнодорожного пути между пунктами А и В, если масса одного метра рельса равна 50 кг, а расстояние между этими пунктами составляет 100 км.
1). 5 · 10 6 кг; 2). 10 7 кг; 3). 5 · 10 9 кг; 4). 10 10 кг.
2. Найдите значение выражения 
при х = 0,8.
Ответ: __________
3. Число т, являющееся средним квадратическим двух чисел a и b, определяется по формуле 
. Выразите из этой формулы число b.
1). 
; 2). 
; 3). 
; 4). 2 т 2 – а 2.
4. Третий член геометрической прогрессии равен 1, шестой равен 
.
Найдите девятый член прогрессии.
1). 64; 2). 0,125; 3). 
; 4). 
.
5. Упростите выражение 
.
1) 
; 2) 
; 3) 
; 4) 
.
6. Для каждого выражения из верхней строки укажите равное ему выражение из нижней строки:
1). 
2). (а – 1 · 
) 4; 3). 
; 4). (а 3 · ) -2 .
а). а – 2; б). а – 3; в). а 8; г). а 9.
7. Разложите на множители выражение: (х 2 – 16) (х + 3) – 4(х – 4) (х + 3).
Ответ: ___________
8. Выполните умножение: 
· (т 2 – тп + п 2).
1). п – т; 2). т – п; 3). 
; 4). 
.
9. Найдите произведение корней уравнения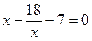 
.
1) 18; 2). – 18; 3). 24; 4). 9.
10. На счет в банке, доход по которому составляет 25 % годовых, внесли т рублей. Какая сумма будет на счету через год?
1). 0,25 т р; 2). т + 0,25 т р; 3). т + 25 т р; 4) т + 25 р.
11. Бабушка старше мамы на 20 лет, а мама старше дочери в 5 раз. Вместе им 86 лет. Сколько лет дочери?
1). 6 лет; 2). 16 лет; 3). 11 лет; 4). 12лет.
12. Найдите наименьшее целое положительное решение системы неравенств: 
Ответ: ____________
13. Вычислите координаты точки пересечения прямых 5 х + 3 у = - 11 и 7 х + 2 у = 0.
1) (- 7; 2); 2). (7; - 2); 3). (2; - 7); 4). (- 2; 7).
14. Найдите область определения функции f (х) = 
.
1). (- ∞; - 4) 
(0; 4); 2). [- 4; 0) [4; + ∞); 3). [- 4; 4]; 4). (- ∞; - 4] [4; + ∞).
15. Разложите на множители квадратный трехчлен: 13 – 5 х 2 – 8 х.
1). 5(х – 1) (х – 2,6); 2). (х – 1) (5 х – 13); 3) - 5(х – 1) (х + 2,6);
4). 5(х – 1) (х – 2,6).
16. Найдите сумму расстояний от вершины параболы у = х 2 – 6 х + 5 до координатных осей.
1). – 1; 2). – 7; 3). 1; 4). 7.
Часть 2. Задания этой части выполняйте с записью решения.
1. (2 балла). Решите неравенство: (3 х + 7) (1 – х) < 3.
2. (4 балла). Решите уравнение: 
.
3. (4 балла). Две бригады, работая вместе, могут закончить свою работу за 8 дней. Если первая бригада будет работать 3 дня, а вторая 12 дней, то они выполнят 75 % всей работы. За сколько дней может выполнить работу каждая бригада, работая отдельно?
4. (6 баллов). Решите уравнение: х 2 – 2 | х | - 3 = 0.
5. (6 баллов). При каких значениях параметра т уравнение тх 2 – (т – 7) х + 9 = 0 имеет два равных отрицательных корня?
Вариант 13.
Часть1.
1. Вычислите: 
· 1,2– 0,5 2: 
.
1). 0,15; 2). – 0,45; 3). – 4,5; 4). 1,05.
2. Упростите выражение: - 21 у 2 · 
.
1). – 49 у 4; 2). 
; 3). 
; 4) 
.
3. Укажите набольший корень уравнения: 3 х 2 + 5 х – 2 = 0.
1). 4; 2). 2; 3). 
; 4). .
4. Решите уравнение: 
.
Ответ: ________
5. Какие из указанных неравенств не имеют решений?
а). х 2 - 8 х + 16 ≤ 0, б).4 х 2 + х + 1 < 0, в).- | х | - 3 > х 2, г).(х – 3)2 (х + 3) < 0.
1). в, г;2). а, б, г;3). а, б, в;4). б, в.
6. Сколько процентов составляет число 32 от своего квадрата?
Ответ: ___________
7. Найдите сумму первых восьми членов арифметической прогрессии, в которой
а 1 = 24,5, а 7 = 33,5.
1). 347,1; 2). 148,8; 3). 297,6; 4). 238.
8. Найдите наименьшее целое значение х, при котором функция у = 3 х 2- 2 х – 5 принимает отрицательные значения.
1). – 1; 2). 0; 3). – 2; 4). – 1.
9. Найдите произведение х 0 у 0, если х 0и у 0, - решения системы уравнений: 
1). - 8; 2) 6; 3). – 10; 4). 12.
10. Найдите область определения функции f (x) =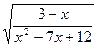 
.
1). (- ∞; 3) (3; 4); 2). (- ∞; 3] [3; 4); 3). (- ∞; 3]; 4). (- ∞; 3) (3; 4].
11 В школьную библиотеку поступили учебники по алгебре и геометрии, среди которых учебников по алгебре 216, что составляет 25 % полученных учебников. Сколько учебников по математике поступило в библиотеку?
Ответ: __________
12. Функция задана графиком. Укажите множество значений этой функции.
 |
1) 
; 2) 
; 3) 
; 4) 
.
13. Решите неравенство: - 3,6 < 2 х – 3 < 4.
1). (- 0,3; 3,5); 2).(- ∞; - 0,3) (7; + ∞); 3)..(- ∞; - 0,3); 4); [- 0,3; 3,5].
14. Разложите на множители выражение: ас – ас 2:
1). с (1 – а) (1 + а); 2). ас (1 + с); 3). а (1 – с) (1 + с); 4). ас (1 - с).
15. Велосипедист каждую минуту проезжает на 800 м меньше, чем мотоциклист, поэтому на путь в 30 км он затратил времени на 2 ч больше, чем мотоциклист. Сколько километров в час проезжает мотоциклист?
Ответ: _____________
16. Среди данных чисел укажите корень шестой степени из числа 729.
1). 63; 2). 27; 3). 6; 4). 3.
