К экзамену.
Задачи на исследование уравнений и неравенств (4 балла).
1 Укажите промежуток, которому принадлежат корни уравнения  .
.
1) 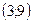 2)
2) 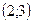 3)
3)  4)
4) 
2 Укажите промежуток, которому принадлежат корни уравнения 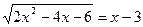 .
.
1) 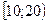 2)
2) 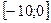 3)
3)  4)
4) 
3 Укажите промежуток, которому принадлежат корни уравнения 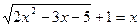 .
.
1)  2)
2)  3)
3)  4)
4) 
4 Укажите промежуток, которому принадлежат корни уравнения  .
.
1).  2).
2).  3).
3).  4).
4). 
5 Укажите промежуток, содержащий корни уравнения  .
.
1).  2).
2).  3).
3).  4).
4). 
6 Укажите промежуток, содержащий корни уравнения  .
.
1).  2).
2).  3).
3). 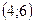
 4).
4). 
7 Укажите промежуток, содержащий корни уравнения 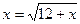 .
.
1).  2).
2). 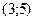 3).
3).  4).
4). 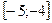
8 Укажите промежуток, содержащий корни уравнения  .
.
1).  2).
2).  3).
3). 
 4).
4). 
9. Какому промежутку принадлежат корни уравнения 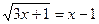 ?
?
1). 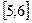 2).
2). 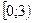 3).
3).  4).
4). 
11 Определите число целых решений неравенства  .
.
1). 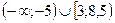 2).
2).  3).
3). 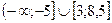
4). 
12 Решите неравенство  .
.
1).  2).
2). 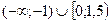 3).
3). 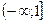 4).
4). 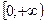
13 Определите число целых решений неравенства  .
.
1).  2).
2).  3).
3). 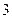 4).
4). 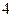
14 Определите число целых неотрицательных решений неравенства  .
.
1). 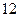 2).
2).  3).
3).  4).
4). 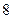
15 Решите неравенство  .
.
1).  2).
2). 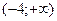 3).
3).  4).
4). 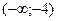
16 Решите неравенство  .
.
1).  2).
2). 
3)  4).
4). 
17 Решите неравенство  .
.
1).  2).
2). 
3).  4).
4). 
18 Решите неравенство  .
.
1). 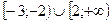 2).
2). 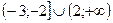
3).  4).
4). 
Неравенства (4 балла).
1 Решите неравенство 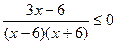 .
.
1).  2).
2). 
3).  4).
4). 
2 Решите неравенство 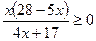 .
.
1).  2).
2). 
3). 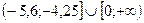 4).
4). 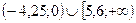
3 Решите неравенство  .
.
1). 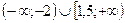 2).
2). 
3).  4).
4). 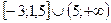
4 Решите неравенство  .
.
1).  2).
2). 
3).  4).
4). 
Преобразование выражений (2 балла)
Упростить выражения.
1.  2.
2. 

3. 
 4.
4.  ∙ 0,5
∙ 0,5
5.  6.
6. 
7. (а -2 – с -2) (с -1 – а -1)—1 8.  ∙
∙ 
9. 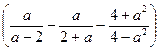 ∙
∙ 
10. 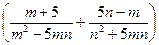 ∙
∙ 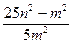
11.  :
: 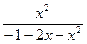 12.
12.  : 1,2
: 1,2
13. 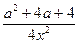 :
: 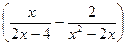 14.
14. 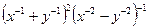
15.  16.
16.  ∙
∙ 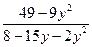
17.  ∙
∙  18.
18. 
19.  ∙
∙  20.
20. 
21. 
22. 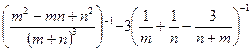
23.  24.
24. 
25.  ∙
∙  26.
26. 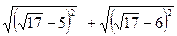
27. 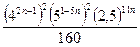 28.
28.  ∙
∙ 
29. 
30. 
Решите уравнения (4 балла).
1.  2.
2. 
3. х 4 – 5 х 2 – 36 = 0 4. 10 х 4 – 45 х = 30 х 2 – 15 х 3
5. 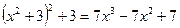 6. 5 х 3 + 3 х 2 – 5 х – 3 = 0
6. 5 х 3 + 3 х 2 – 5 х – 3 = 0
7.  8.
8. 
9.  10.
10. 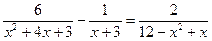
11.  12.
12. 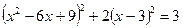
13.  ∙
∙  = 0 14.
= 0 14.  ∙
∙ 
15.  16..
16.. 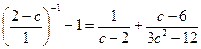
17. 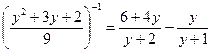 18.
18. 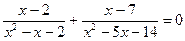
19.  20.
20. 
21.  22.
22. 
23.  24..
24.. 
25.  26.
26. 
27.  28.
28. 
29.  30.
30. 
31.  32.
32. 
33. 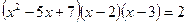 34.
34. 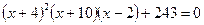
35.  36.
36. 
37.  38.
38. 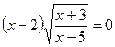
39.  40. 2 х 4 – 5 х 3 + 2 х 2 – 5 х = 0
40. 2 х 4 – 5 х 3 + 2 х 2 – 5 х = 0
41. Найдите сумму действительных корней уравнения | х 2 + 2 х | = 1
42. | х 2 + 4 х | = 4 43. | х + 2 | = 2(3 – х)
44. | 3 х - 1 | = 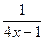 45. | 5 х + 2 | = 3-3 х
45. | 5 х + 2 | = 3-3 х
46. Пусть х корень уравнения  , тогда значение 2 х 2 – 7 х +1 равно
, тогда значение 2 х 2 – 7 х +1 равно
1). – 2; 2). 9; 3). -5; 4).1; 5). 10.
5. Решите систему уравнений (4 балла).
1.  2.
2.  3.
3. 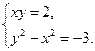 4.
4. 
5.  6.
6.  7.
7.  8.
8. 
6. Решите неравенства (4 балла).
1.  2.
2. 
3.  < -
< -  4. 0 < 1 +
4. 0 < 1 + 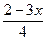 < 4
< 4
5.  6.
6. 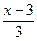 >
> 
7. (2с – 5) (с + 3) > (с – 7) (5 + 3с) 8. 8у + 1 + 15 у2 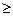 0
0
9. 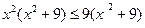 10.
10.  < - х – 4
< - х – 4
11.  < - х – 7. Укажите наибольшее целое значение х.
< - х – 7. Укажите наибольшее целое значение х.
12.  13.
13.  14.
14. 
15.  16.
16.  17.
17. 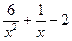 < 0
< 0
18.  <
<  19.
19.  > 2 -
> 2 -  20.
20. 
21.  22.
22.  23.
23.  < 0
< 0
24. Найдите сумму целых отрицательных решений неравенства 
25. Найдите сумму целых положительных решений неравенства 1+ 
26.  27.
27.  < 0
< 0
28.  29.
29.  30.
30. 
31. 
32. Найдите все целые значения переменной у, при которых имеет смысл выражение 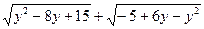 .
.
33. Найдите наибольшее целое значение переменной а, при котором имеет смысл выражение 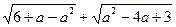 .
.
34. Найдите наименьшее целое решение неравенства  > 0
> 0
35. Найдите наименьшее целое решение неравенства 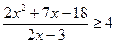
36. Найдите наименьшее целое решение неравенства 
37. Найдите наименьшее целое решение неравенства 2 – х > 
Задания высокого уровня трудности (6 баллов).
Упростите выражение.
1.  2.
2. 
3. 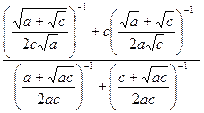

4.  . Сравните с
. Сравните с 
5. 
6. 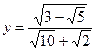 .Сравните с
.Сравните с 
Решите уравнения.
1. Для каждого значения параметра р решите уравнение 
2. Найдите все значения параметра т, при которых уравнение 
имеет один корень.
Решите систему уравнений
1  2.
2.  3.
3. 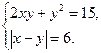
4. 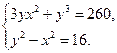 5.
5. 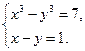 6.
6. 
7.  8.
8.  9.
9. 
10.  11.
11. 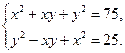 12.
12. 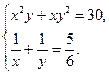
13. 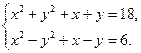 14.
14.  15.
15. 
16.  17.
17. 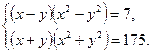 18.
18. 
19.  20.
20.  21.
21. 
22.  23.
23.  23.
23. 
24.  25.
25. 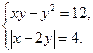 26.
26. 
27. 
 28.
28.  29.
29.  .
.
30. 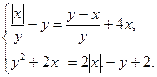 31.
31. 
32. 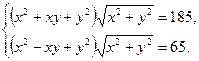
Решите неравенства.
1.  2.
2.  < 0 3.
< 0 3. 
4. 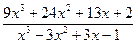 > 0 5.
> 0 5.  6.
6. 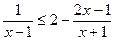
7.  8.
8.  > 0
> 0
9. 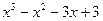 > 0 10.
> 0 10.  > 0 11.
> 0 11. 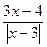 > 2 12.
> 2 12.  < 1
< 1
13.  14.
14.  < 0 15.
< 0 15. 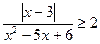 16.
16. 
17. 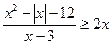 18.
18.  < 3 19.
< 3 19. 
20. 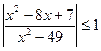 21.
21. 
22.  23.
23. 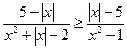 . 24.
. 24. 
25. Найти все решения неравенства 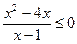 , для которого выполняется неравенство (х 3 – 1) (3 – х) ≥ 0.
, для которого выполняется неравенство (х 3 – 1) (3 – х) ≥ 0.
26. Найти наибольшее целое отрицательное решение неравенства
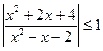 2
2
27. При каких значениях параметра т неравенство  > 3 не имеет решений?
> 3 не имеет решений?
28. При каких значениях параметра а неравенство  < 3 не имеет решений?
< 3 не имеет решений?
29. Для каждого значения параметра т решите неравенство 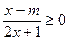 .
.
30. Для каждого значения параметра т решите ситстему неравенств 
32. Найдите все значения параметра а, при котором система неравенств 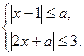 имеет единственное решение.
имеет единственное решение.
Решите систему неравенств.
1.  2.
2.  3.
3. 
8. Прогрессии.






