Пусть задан алфавит V.
 — множество всех слов в алфавите V.
— множество всех слов в алфавите V.
Формальный язык L в алфавите V — произвольное подмножество  .
.
 — грамматика, где
— грамматика, где
V — основной алфавит;
W — вспомогательный алфавит;

I — начальный символ,  ;
;
R — множество правил вывода, вида  , где
, где  .
.


| слово b есть непосредственное следствие слова a, если 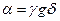 , , 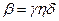 и существует правило и существует правило  слово b выводимо из слова a, если существует последовательность слов
слово b выводимо из слова a, если существует последовательность слов  такая что для всех такая что для всех  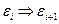 , т.е. каждая , т.е. каждая  есть непосредственное следствие есть непосредственное следствие  (n — длина вывода). (n — длина вывода).
|
Язык грамматики — множество всех слов в алфавите V, выводимых из начального символа I.
 ;
; 
Грамматики G и G1, называются эквивалентными, если  их языки совпадают.
их языки совпадают.
Пример: грамматика нечетных чисел.

 — язык грамматики
— язык грамматики





Теория автоматов. Теория автоматов изучает абстрактные машины в виде математических моделей, и проблемы, которые они могут решать.
Автоматом называется дискретный преобразователь информации, способный принимать различные состояния, переходить под воздействием входных сигналов из одного состояния в другое и выдавать выходные сигналы.
Если множество состояний автомата, а так же множества входных и выходных сигналов конечны, то автомат называется конечным автоматом.
Математической моделью реального конечного автомата является абстрактный автомат, который имеет один входной канал и один выходной канал.


|
Автомат — последовательность (кортеж) из пяти элементов (Q,Σ,δ,S0,F), где:
- Q — конечное множество состояний автомата – алфавит состояний
- Σ — алфавит языка, который понимает автомат, (входной и выходной алфавит)
- δ — функция перехода, такая что

- S0 — начальное состояние, состояние когда автомат еще не прочитал ни одного символа
- F — множество состояний, называемое «конечные состояния».
Можно утверждать, что язык L, который читается автоматом M, состоит из множества слов w на базе алфавита Σ, так что если эти слова вводятся в M, он приходит в одно из состояний F:

отдельные символы, образующие алфавит – буквы, а любые упорядоченные последовательности букв данного алфавита – слова в этом алфавите.
Например. В алфавите X = (x1, x2), состоящем из двух букв, словами будут: x1, x2, x1x1, x1x2, x2x1,x2x2, x1x1x1, и т.д.
d - функция переходов, определяющая состояние автомата a(t+1), в котором автомат будет находиться в момент времени (t+1), в зависимости от состояния автомата a(t) и входного сигнала x(t) в момент времени t, т.е. a(t+1) = d [a(t),x(t)], l - функция выходов, определяющая значение выходного сигнала y(t) в зависимости от состояния автомата a(t) и входного сигнала x(t) в момент времени t, т.е. y(t) = l[a(t), x(t)].
Автомат функционирует в дискретные моменты времени, интервал между которыми Т называется тактом. При этом в каждый дискретный момент времени на вход автомата поступает одна буква входного алфавита, автомат переходит из одного состояния в другое и выдается одна буква выходного алфавита. В зависимости от того, как задается длительность такта Т, различают автоматы синхронного действия (T = const) и асинхронного действия (T ¹ const).
Детерминированный автомат – автомат каждой паре символов q(t) и x(t) ставит в однозначное соответствие пару символов q(t+1) и y(t).
Вероятностные или стохастические автоматы, в которых переход из одного состояния в другое под воздействием случайных или детерминированных входных сигналов происходит случайно. Работа таких автоматов описывается уже матрицей переходов d, элементами которой являются вероятности переходов из одного состояния в другое.
Применяемые на практике автоматы принято разделять на два класса: - это автоматы Мили и автоматы Мура.
Отличительной особенностью автоматов Мили является то, что их выходные сигналы зависят как от состояния автомата, так и от значения входного сигнала. В автоматах Мура выходные сигналы y(t) в каждый дискретный момент времени t однозначно определяются состоянием автомата в тот же момент времени и не зависят от значения входного сигнала.






