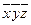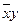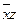- По таблице истинности перебираем все импликанты (по единичным наборам);
- Оставляем простые импликанты.
- Применяем таблицу покрытия.
Пример:
|
a) длины 3 |
б) длины 2 |
в) длины 1 |


Таблица покрытия:

| |||||

|
4. изоморфизм между алгеброй множеств и алгеброй логических векторов

 Эти две алгебры изоморфны, если существуют:
Эти две алгебры изоморфны, если существуют:
1. отображение  , такое что j взаимно однозначное соответствие.
, такое что j взаимно однозначное соответствие.
2. сохранение операций 
 —булеан
—булеан
 —булева алгебра;
—булева алгебра;
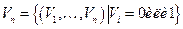
 —алгебра логических векторов.
—алгебра логических векторов.



I-ая теорема об изоморфизме: Алгебра множеств изоморфна алгебре логических векторов.
Доказательство:
Пусть 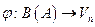
В(А) – мн-во, где А= {а1, …, аn }
Vn – мн-во двоичных векторов длины n.
Каждому подмножеству МÍA соответствует двоичный вектор φ(М) = V = (V1, … Vn), где


1 φ (М1 È М2) = 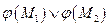
2 φ (М1 Ç М2) = 
3 φ ( ) =
) = 
Пусть i-ая компонента вектора φ (М1 È М2) равна 1 Þ аiÎ М1 È М2 Þ аiÎ М1 или аiÎ М2 Þ
i-ая компонента вектора φ (М1)=1 или i-ая компонента вектора φ (М2)=1 Þ i-ая компонента вектора φ(М1)Ú φ (М2)=1.
Пусть i-ая компонента вектора φ (М1 È М2) равна 0 Þ 
 и
и  Þ
Þ
i-ая компонента вектора φ (М1)=0 и i-ая компонента вектора φ (М2)=0 Þ i-ая компонента вектора φ(М1)Ú φ (М2)=0.
5. Теорема Шеннона, полнота системы булевых функций.
булевой функцией называют функцию типа Bn ==>B, B={0,1} где — булево множество, а n — неотрицательное целое число, которое называют арностью или местностью функции. Элементы 1 (единица) и 0 (ноль) стандартно интерпретируют как истину и ложь, хотя в общем случае их смысл может быть любым. Элементы Bn называют булевыми векторами. В случае n = 0 булева функция превращается в булеву константу.
Теорема Шеннона:
Любую булеву функцию можно представить в виде 
Доказательство:
Пусть  – фиксированный набор. Подставим в левую и правую части, получим
– фиксированный набор. Подставим в левую и правую части, получим

Следствие: при n = k.

где дизъюнкция берется по веем наборам (s1, …, sn), на которых f(s1, …, sn) = 1. Это СДНФ.
Следствие (двойственная теорема Шеннона): если заменить дизъюнкцию на конъюнкцию, то 
при n = k

где конъюнкция берется по всем наборам (s1, …, sn), на которых f(s1, …, sn) = 0. Это СКНФ.
Полнота системы булевых функций. Система å называется полной, если при помощи суперпозиции из этого множества функций можно получить все булевы функции.
Примеры полных систем:

Суперпозицией множества функций, называется подстановка функций друг в друга.
Теорема. Отрицание, дизъюнкция и конъюнкция образуют полную систему булевых функций
Полная система булевых функций называется базисом, если она перестает быть полной при удалении хотя бы одной из этих функций.
Согласно этому определению система булевых функций не является базисом. Действительно, применяя законы де-Моргана, конъюнкцию в булевой функции можно заменить на дизъюнкцию и отрицание, а дизъюнкцию - на конъюнкцию и отрицание. Следовательно, отрицание и дизъюнкция (отрицание и конъюнкция) также образуют полную систему булевых функций. Нетрудно убедиться, что наборы и являются базисными, так как их дальнейшее сокращение без нарушения полноты системы невозможно.