Граф является эйлеровым тогда и только тогда, когда он связен и все степени его вершин четны.
Теорема. Граф является полуэйлеровым тогда и только тогда, когда в нем не более двух вершин(одной вершины не может быть из леммы о рукопожатиях).
Граф называется гамильтоновым графом, если он содержит цикл, проходящий через каждую вершину ровно один раз.
 |
Если цикл заменить на произвольный путь, то это будет полугамильтоновый граф.
Сети.
Ориентированный граф G =(V,A) - пара множеств V и A, таких, что V - некоторое конечное непустое множество, а A - некоторое подмножество декартового квадрата V(AÍ V2 = V * V).
Вершины графа G - элементы множества B.
Дуги графа G - элементы множества A.
Дуга - упорядоченная пара вершин a=(u,v). Начало дуги - вершина u, конец дуги - вершина v. Дуга исходит из своего начала и заходит в свой конец.
Орграф G - орграф p-го порядка, если мощность множества |V|=p.
Полустепень захода вершины v графа G - число дуг, заходящих в вершину v:
deg- (v) = | X |; X = { x | x = (u,v) ÎA}.
Полустепень исхода вершины v графа G - число дуг, исходящих из вершины v:
deg+ (v) = | Y |; Y = { y | y = (v,u)Î A}.
Степень вершины v графа G - сумма полустепеней захода и исхода в вершине v:
deg (v) = deg+(v) + deg-(v).
Сеть - это некоторый нагруженный смешанный орграф, в котором выделены 2 вершины:
вершина S - это вершина с нулевой полустепенью захода является истоком графа,
вершина t - это вершина с нулевой полустепенью захода сток графа.
Каждой дуге (ij) орграфа G поставлено в соответствие некоторое число (положительное) bij, которое называется пропускной способностью дуги.
Под потоком в сети будем понимать xij, если выполняется следующее условие:
1. xij по дуге 0 ≤ xij ≤ bij.
2. Для каждого промежуточного узла i ≠ S ≠ t выполняется закон Кирхгофа, т. е. поток в промежуточном узле не теряется и не увеличивается.
 ∑kxki=∑jxij
∑kxki=∑jxij
Вычисление максимального потока через сеть, раскраска вершин и ребер графов;
Сети.
Ориентированный граф G =(V,A) - пара множеств V и A, таких, что V - некоторое конечное непустое множество, а A - некоторое подмножество декартового квадрата V(AÍ V2 = V * V).
Вершины графа G - элементы множества B.
Дуги графа G - элементы множества A.
Дуга - упорядоченная пара вершин a=(u,v). Начало дуги - вершина u, конец дуги - вершина v. Дуга исходит из своего начала и заходит в свой конец.
Орграф G - орграф p-го порядка, если мощность множества |V|=p.
Полустепень захода вершины v графа G - число дуг, заходящих в вершину v:
deg- (v) = | X |; X = { x | x = (u,v) ÎA}.
Полустепень исхода вершины v графа G - число дуг, исходящих из вершины v:
deg+ (v) = | Y |; Y = { y | y = (v,u)Î A}.
Степень вершины v графа G - сумма полустепеней захода и исхода в вершине v:
deg (v) = deg+(v) + deg-(v).
Сеть - это некоторый нагруженный смешанный орграф, в котором выделены 2 вершины:
вершина S - это вершина с нулевой полустепенью захода является истоком графа,
вершина t - это вершина с нулевой полустепенью захода сток графа.
Каждой дуге (ij) орграфа G поставлено в соответствие некоторое число (положительное) bij, которое называется пропускной способностью дуги.
Под потоком в сети будем понимать xij, если выполняется следующее условие:
1. xij по дуге 0 ≤ xij ≤ bij.
2. Для каждого промежуточного узла i ≠ S ≠ t выполняется закон Кирхгофа, т. е. поток в промежуточном узле не теряется и не увеличивается.
 ∑kxki=∑jxij
∑kxki=∑jxij
(сколько входит, столько выходит)
3. Величина потока, исходящая из источника является величиной потока, входящая в сток
∑kxki=∑xit
Величиной потока x называется 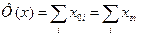
Задача о максимальном потоке заключается в определении потока максимальной величины1.
Разрезом W в сети называется любое множество вершин, обязательно содержащее выход и не содержащее вход. Пропускной способностью C (W) разреза W называется сумма пропускных способностей дуг, заходящих в разрез.
Известно, что величина любого потока не превышает пропускной способности любого разреза (теорема Форда-Фалкерсона).
Следовательно, если удастся найти поток, величина которого равна пропускной способности некоторого разреза, то этот поток максимален, а разрез минимален.
Алгоритм 7 (алгоритм Форда-Фалкерсона). Применение алгоритма проиллюстрируем примером сети, приведенной на рисунке 3, в которой пропускные способности всех дуг равны единице.
Шаг 0. Берем произвольный поток (например, поток x01 = x12 = x25 = 1). Помечаем начальную вершину индексом «0».
Обозначим Z – множество помеченных вершин.
Общий шаг. Первое действие. Помечаем вершину j индексом + i, если, во-первых, существует дуга (i; j), и, во-вторых, i I Z, j I Z, xij < Cij.

Если в результате этого типа пометок мы пометили выход, то поток можно увеличить хотя бы на единицу (если cij – целые числа). Двигаясь обратно, можно найти путь, поток по которому можно увеличить. Однако, как видно из примера, этого недостаточно для нахождения максимального потока.
Второе действие. Помечаем вершину i индексом -j, если, во-первых, существует дуга (j; i), и, во-вторых, j I Z, i I Z, xij > 0 (легко видеть, что пометки первого типа увеличивают поток по
дуге, а пометки второго типа – уменьшают). Если в результате этого типа пометок мы пометили выход, то поток можно увеличить. Двигаясь обратно, можно найти цепь, в которой каждая вершина помечена номером предыдущей (знак пометки не важен).
Рассмотрим цепь m = (0; 3; 2; 1; 4; 5), приведенную на рисунке 3. Полученные в результате второго действия потоки обозначены жирным шрифтом. Критерий остановки алгоритма следующий: если, применяя пометки обоих типов, вершину n пометить не удалось, то полученный поток имеет максимальную величину.
Раскраска графов.
граф G неориентированный и пусть k - натуральное число. Тогда k-раскраской графа G называется произвольная функция f, отображающая множество вершин графа G в некоторое k-элементное множество:
f: V→{a1, a2,..., ak} = A
В качестве элементов множества A чаще всего используется отрезок натурального ряда {1, 2,..., k} либо {a, b,..., n} или краски типа {синий, красный,:, черный}.
Раскраска называется правильной, если f(u) ≠ f(v) для любых смежных вершин u и v графа G.
Хроматическое число графа G - это минимальное число красок, при котором граф имеет правильную раскраску. Если хроматическое число равно k, то граф называется k-хроматическим (обозначают λ(G) = k).
Для полного графа Kn хроматическое число равно:
λ(Kn) = n,
Для пустого: λ(0n) = 1.
Раскраска ребер.
Пусть есть G = (V, E), где |V| = p, |E| = q. Тогда реберной k-раскраской называется некоторая функция j, задающая отображения множества E, т. е.
φ: E → A = {a1,..., ak}
Граф называется k-раскрашиваемым, если существует правильная раскраска ребер.
Минимальное число k, при котором существует правильная реберная k-раскраска называется реберным хроматическим числом или индексом.
Граф G называется реберно k-хроматическим, если хроматический индекс равен k.






