Свойства операций над множествами

Дискретка.

Множеством будем называть некоторую совокупность элементов произвольного рода.

А В={x│x A или x B}- объединение

А В={x│x A и x В} - пересечение

A\B={x│x A и x B}- разность

Ā=U\A - дополнение

Множество В является подмножеством множества А, если всякий элемент В является элементом А.

Симметрическая разность.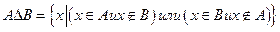

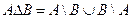
Свойства операций над множествами.

Пусть задан универсум U. Тогда A, B, C U выполняются следующие свойства

1. идемпотентность:

А А=А, А А=А

1. коммутативность:

А В=В А, А В=В А

3. ассоциативность:

А (В С)=(А В) С, А (В С)=(А В) С

1. дистрибутивность:

А (В С)=(А В) (А С), А (В С)=(А В) (А С)

1. инволютивность (правило двойного отрицания):

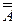=А

1. правило де Моргана:

= , =

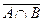1. правило склеивания:

(А В) (А )=А, (А В) (А )=А

1. правило поглощения:

А (А В) =А, А (А В) =А

1. действия с константами:

Константа – универсальное, пустое множество.

А = ; А =U

1. Фундаментальные алгебры, бинарные отношения и их свойства;

Отображение, хⁿ→Х называется n-местной операцией. При n=2 – бинарная операция:х²=хRх→х

Множество А вместе с заданной на нем совокупностью операций, т.е. называется алгеброй. Примеры.

1. Алгебра называется полем действительных чисел.

2. На множестве целых чисел определены операции сложения и умножения по модулю n (остатки от деления на n).

Типы алгебр:

1. Полугруппой называется алгебра с одной операцией и свойством ассоциативности.

a(bc)=(ab)c

В общем случае ab≠ba, если же умножение коммутативно, то полугруппа называется коммутативной. Если полугруппа содержит такой элемент е, что для любого а ае=еа=а, то е называется единицей. Единица в полугруппе всегда единственна.

Пример:

2/3 N не алгебра (операция не должна выходить за рамки основного множества.)

2. Группой называется непустое множество с одной бинарной алгебраической операцией, если выполняются следующие условия:

1) ассоциативность (ab)c=a(bc)

2) 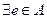, т.е. еа=ае=а, а А

3) а А а^-1 А, аа^-1= а^-1а=е

Число элементов группы называется порядком группы.

Пример группы:

1. Алгебра 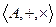с двумя бинарными операциями называется кольцом, если

1. коммутативная группа

2. полугруппа

3. a(b+c)=ab+ac

(b+c)a=ba+ca дистрибутивность

 

1. Алгебра 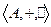называется полем, если

1. коммутативная группа с единицей

2. коммутативная группа

3. a(b+c)=ab+ac

Отношение — математическая структура, которая формально определяет свойства различных объектов и их взаимосвязи. Отношения обычно классифицируются по количеству связываемых объектов (арность) и собственным свойствам (симметричность, транзитивность и пр.). В математике примерами отношений являются равенство (=), коллинеарность, делимость и т. д.

n-местным (n-арным) отношением, заданным на множествах M₁, M₂, … M_n, называется подмножество прямого произведения этих множеств.

Бинарные отношения. Бинарным отношением на множестве M называется подмножество R декартова квадрата M´M (т. е. подмножество множества всех упорядоченных пар элементов из M). xRy означает, что (x,y)ÎR.

Суждения типа "Иван - сын Петра", "Татьяна старше Алексея", "Воронеж южнее Москвы", <Слова "ночь" и "день" содержат одинаковое число букв> приводят к бинарным отношениям на подходящем множестве. Например, последнее суждение определяет бинарное отношение R на множестве X всех слов: xRy, если число букв в словах x и y одинаково.

Свойства отношений.

А - множество, R - отношение на А.

1) R - рефлексивно, если для любого хÎА имеем хRх, т.е. х находится в отношении сам с собой.

2) R - симметрично, если хRy ==> yRх.

3) R - антирефлексивно, если не существует хÎА: хRх, т.е. R выполняется только для не совпадающих элементов.

4) R - не рефлексивно, если существует хÎА такой, что (х,х) не принадлежит R.

5) R - асимметрично, если из xRy и yRx хотя бы одно не выполняется.

6) R - антисимметрично, если для любых (x,y)ÎА из того, что xRy и yRx ==> х=y (≤).

7) R - транзитивно, если для любых x,y,z ÎA выполняется: из xRy и yRz ==> xRz.

Рефлексивное, симметричное и транзитивное отношение на множестве X называется отношением эквивалентности на множестве X.

Отношение строгого порядка – это бинарное отношение на множестве Х, удовлетворяющее следующим условиям:

1. Х<Х – антирефлексивность

2. Х<У и У<Х – несимметричность

3. Х<У и У<Z ® Х<Z - транзитивность

Отношение нестрогого порядка – это бинарное отношение на множестве Х, удовлетворяющее следующим условиям:

1. Х£Х – рефлексивность

2. Х£У и У£Х®Х=У – антисимметричность

3. Х£У и У£Z ® Х£Z – транзитивность