Анализ графической интерпретации функции с выраженным максимальным значением (рис. 8.11 а) показывает, что основа расчета – типовой циклический процесс.
Аналитический расчет (табличное задание) аргумента хi позволяет получить последовательность текущих значений функции yi.
Идея (методика) последовательного сравнения текущих значений функции yi формулируется следующим образом:
присвоить до входа в цикл искомому ymax наименьшее из возможных численных значений
ymax = –1х1020;
сравнить в теле цикла текущее (вначале первое) значение yi с максимальным ymax
yi > ymax;
присвоить максимальному значению ymax текущее yi, если условие выполнено
ymax = yi;
оставить ymax без изменения, если условие не выполнено;
выполнять последние три пункта в каждом повторении цикла.
Внимание! Предлагаемая методика позволяет выполнять поиск максимального значения функции без учета условия существования экстремума (точки изменения возрастания функции на убывание или наоборот).
Словесная формулировка метода поиска максимального значения реализуется смешанным вычислительным процессом взаимодействия внешнего цикла с вложенной типовой схемой алгоритма неполного ветвления:
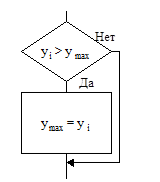
В результате по окончании циклического процесса переменной ymax будет присвоено наибольшее из всех значений yi.
Рассмотрим методику вычисления максимального значения на конкретной задаче (8.7) о частотных характеристиках.
Постановка задачи
Для получения частотных характеристик системы автоматического управления на её вход подаётся синусоидальное возмущающее воздействие: yi = sin xi. Определить максимальное значение yi, если известно, что xi меняется в диапазоне от xн = 0,38 до xк = 1,96 с шагом Dx = 0,11.
Формирование математической модели
Исходные данные
| xн = _ _,_ _ | – начальное значение аргумента; |
| xк = _ _,_ _ | – конечное значение аргумента; |
| Dx = _ _,_ _ | – шаг изменения аргумента. |
Расчётные зависимости
| xi = xn | – текущее значение аргумента; |
| yi = sin x i | – текущее значение функции; |
| ymax = max(y1, y2,...,yi,...,yk) | – максимальное значение; |
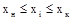
| – диапазон изменения аргумента; |
| x i = x i-1 + Dx | – закон изменения аргумента. |
Выбор метода решения
Математическая формулировка задачи предписывает необходимость вычисления текущих значений функции yi при изменении аргумента xi от xн до xк с заданным шагом Dx.
Параллельно требуется, аналогично методикам накопления (суммирования, умножения), присвоить до входа в цикл искомому ymax наименьшее из возможных численных значений, а в теле цикла осуществить типовое неполное ветвление с проверкой условия yi > ymax, обеспечивающее в одной ветви (условие выполнилось) присвоение ymax нового значения yi (ymax = yi).
В результате по окончании циклического процесса переменной ymax будет присвоено наибольшее из всех значений yi.
Следовательно, в качестве метода решения необходимо выбрать смешанный вычислительный процесс – циклический процесс арифметического типа с аналитическим изменением аргумента, с расположенным внутри его ветвящимся процессом последовательного поиска максимального значения функции.






