Исходные данные
| xн = _,_ мВ | – начальное значение сигнала; |
| xк = _ _,_ мВ | – конечное значение сигнала; |
| Dx = _,_ мВ | – шаг изменения сигнала; |
| k = _,_ | – коэффициент усиления. |
Расчётные зависимости
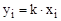
| [мВ = мВ] | – значение выходного сигнала; |

| [ 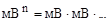 ] ]
| – произведение значений выходного сигнала; |

| [ 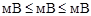 ] ]
| – диапазон изменения входного сигнала; |
| xi = xi-1 + Dx | [мВ = мВ + мВ] | – закон изменения входного сигнала. |
Выбор метода решения
Математическая формулировка задачи определяет, что наряду с вычислением текущих значений выходного сигнала yi необходимо предусмотреть их перемножение. При этом, аналогично рассмотренной ранее методике суммирования, накопление произведения требует выполнение двух операций:
· формирования начального значения произведения (Py = 1) до входа в цикл;
· вычисления в теле цикла текущего значения произведения ( ), которое при выходе из цикла автоматически становится конечным.
), которое при выходе из цикла автоматически становится конечным.
Следовательно, методом решения является смешанный вычислительный процесс – арифметический цикл с аналитическим изменением аргумента с дополнительным накоплением произведения в теле цикла.
Составление алгоритма решения
Математическая модель задачи и выбранный метод решения позволяют выполнить одношаговую схему алгоритма (рис. 8.8).

Рис. 8.8. Схема алгоритма решения задачи 8.4
Выполненный блоком 9 вывод конечного значения искомой переменной облегчает использование результатов, в то время как для отладки предусмотрена печать всех промежуточных (текущих) значений в блоке 7.
Для улучшения наглядности организации вычислений элементы дружественности не показаны.
Программирование задачи
Перед составлением программы решения выполним идентификацию переменных. Ввиду того, что хранение промежуточных результатов не требуется, используем в программе неиндексированные переменные (табл. 8.4).
Таблица 8.4
| Обозначение в алгоритме | xн | xк | Dx | k | xi | yi | Py |
| Обозначение в программе | xn | xk | dx | k | xi | yi | py |
С учётом таблицы идентификации на основании схемы алгоритма составим программы решения задачи.
Классический вариант программирования задачи
#include<stdio.h>
#include<stdlib.h>
#include<math.h>
#include<conio.h>
#include <windows.h>
main()
{
float xn, xk, dx, k, /* описание */
xi, yi; /* локальных */
double py; /* переменных */
char buf[50]; /*описание символьного массива*/
clrscr();
CharToOem("Введите начальное значение сигнала xн (мВ):", buf);
printf("\n %s ",buf);
scanf("%f", &xn);
CharToOem("Введите конечное значение сигнала xк (мВ): ", buf);
printf("\n %s ",buf);
scanf("%f", &xk);
CharToOem(" Введите шаг изменения сигнала dx (мВ): ",buf);
printf("\n %s ",buf);
scanf("%f", &dx);
CharToOem(" Введите коэффициент усиления сигнала k: ",buf);
printf("\n %s ",buf);
scanf("%f", &k);
py = 1.;
printf("\n ----------------------------------------"
"\n | xi, | yi, | Py |"
"\n | mB | mB | |"
"\n ---------------------------------------");
for(xi = xn; xi <= xk; xi += dx) /* заголовок цикла расчёта */
{
yi = k * xi;
py *= yi;
printf("\n | %4.1f | %4.1f | %20.1lf |", xi, yi, py);
}
printf("\n ----------------------------------------");
printf("\n Py=%.1lf \n", py);
getch();
}
3.7 8.1 0.3 1.5
Под закрывающей скобкой программы приведены численные значения исходных данных для решения задачи.
Результаты решения представлены в приложении 8.7.
Программирование задачи с графическим интерфейсом
Программирование задачи при использовании графического интерфейса предварим его разработкой. Для ввода начального и конечного значений сигнала, шага его изменения и коэффициента усиления сигнала планируем однострочные поля редактирования (EditXn, EditXk, EditDx, EditK). Вывод текущих расчетных значений сигнала и произведения значений сигнала реализуем в поля-списки (ListBoxYi, ListBoxPi).
Управление процессом решения реализуем двумя командными кнопками, расположенными в нижней части окна. Назначение каждой определяется ее названием.
|
|

С учетом планируемого интерфейса выполним программирование задачи.
#include<stdio.h>
#include<stdlib.h>
#include<math.h>
…
void TSumprDlgClient::Ok()
{
// INSERT>> Your code here.
float xn, xk, dx, k, /* описание */
xi, yi; /* локальных */
double py; /* переменных */
char buf[50]; /*описание символьного массива*/
ListBoxYi->ClearList();/*очистка полей*/
ListBoxPi->ClearList();/*вывода*/
EditXn->GetText(buf, 10); /*ввод начального*/
xn = atof(buf); /* значения сигнала*/
EditXk->GetText(buf, 10); /*ввод конечного*/
xk = atof(buf); /* значения сигнала*/
EditDx->GetText(buf, 10); /*ввод шага*/
dx = atof(buf); /* изменения сигнала*/
EditK->GetText(buf, 10); /*ввод коэффициента*/
k = atof(buf); /* усиления сигнала*/
py = 1.;/*формирование начального значения произведения*/
for(xi = xn; xi <= xk; xi += dx) /* заголовок цикла расчёта */
{
yi = k * xi;/*текущее значение сигнала на выходе*/
py *= yi; /*текущее значение произведения*/
sprintf(buf,"%11.1f",yi); /* вывод текущих*/
ListBoxYi->AddString(buf); /*значений yi*/
sprintf(buf,"%17.1f",py); /* вывод текущих*/
ListBoxPi->AddString(buf); /*значений pi*/
}
}
3.7 8.1 0.3 1.5
Под закрывающей скобкой программы приведены численные значения исходных данных для решения задачи.
Результаты решения представлены в приложении 8.8.






