Следующий типовой вариант накопления сумм – вычисление степенных рядов.
Степенные ряды (цепные дроби) нашли широкое применение в информатике для расчёта тригонометрических и других трансцендентных функций, т.е. решения задач, точное (аналитическое) решение которых невозможно или затруднено. При этом предлагается, используя численный метод разложения функции в степенной ряд (цепную дробь), просчитать приближённое значение этого ряда (дроби) по отношению к истинному (недостижимому) с заданной степенью точности:
Ввиду того, что на самом деле точное значение неизвестно, возникает необходимость в замене этого значения на реально возможное. Для наглядности рассмотрим математическую формулировку гипотетического ряда:
Цель – вычислить (собрать) ряд.
Собрать ряд – просчитать значение суммы составляющих его слагаемых при изменении i в истинном или заданном диапазоне.
Анализ представленного ряда, позволяет сделать вывод, что полная его сборка технически (до бесконечности) невозможна. Поэтому в качестве истинного значения предлагается использовать сумму n значений ряда
.
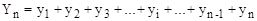Тогда, приняв в качестве истинного значения сумму n элементов ряда, а приближённого – сумму (n – 1) элементов, формула определения степени точности примет вид:
,
или с точки зрения рассматриваемого степенного ряда:
.
Анализ полученного выражения приводит к выводу, что степень точности определяется последним из вычисленных элементов ряда
,
а методом решения должен быть итерационный вычислительный процесс с рекуррентным изменением параметра цикла yi.
Общая методика подготовки к итерационным вычислениям в математике хорошо известна:
определить сходимость ряда;
выбрать метод вычисления текущего значения элемента;
задаться требуемой точностью вычислений;
определить начальные условия (при необходимости).
Определение сходимости выполняется проверкой условия, что каждый последующий элемент ряда по модулю меньше предыдущего (|yn| < |yn-1|). В этом случае ряд сходится (задача имеет решение), в противном – ряд расходится и задача решения не имеет.
В математике разработаны специальные методы предварительной оценки сходимости ряда. В случаях, когда их использование затруднено, осуществляют отладочное решение задачи в течении нескольких циклов с анализом полученных промежуточных значений. Если в результате отладки выявляется тенденция к увеличению модуля текущего значения элемента, процесс относится к расходящемуся и вычисления следует прекратить, в противном случае (ряд сходится) решение продолжается до выполнения условия:
()
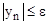Например, анализ ряда
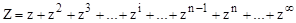
позволяет сделать вывод, что при значениях z < 1 он сходится, в противном случае (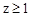
) – расходится. Следовательно, решение возможно, например, при значении z = 0,65, причём уменьшение этого значения увеличивает сходимость и наоборот.
Метод расчёта текущих значений элементов ряда выбирается из двух возможных:
· прямое вычисление текущего значения элемента через текущее значение его индекса (yn = f(n));
· вычисление по рекуррентному соотношению, т.е. аналитической зависимости между последующим и предыдущим элементами yn=f(yn-1).
В большинстве случаев возможно использование только одного из указанных методов, однако, для некоторых рядов (цепных дробей) можно выбирать любой из них.
Для рассматриваемого степенного ряда, возможно использование как прямого вычисления (z5 = z5), так и рекуррентной зависимости (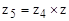
).
Параметр цикла, его начальное значение и закон изменения зависят от выбранного метода расчёта. При расчете напрямую параметром цикла будет индекс (показатель степени) i с начальным значением i = 1 и законом изменения i = i + 1.
При использовании рекуррентной зависимости в качестве параметра цикла необходимо взять текущее значение элемента ряда zi с начальным значением zi-1 = 1 и законом изменения 
. Проанализировав обе зависимости желательно остановиться на первой (прямой), как более простой.
Степень точности определяется с учётом требований конкретной задачи.
Для инженерных задач требуемая степень точности:
e = 10 –4 ¸10 –6
Она позволяет сформировать условие повторения цикла, либо выхода из него. В принципе, желательно использовать несколько вариантов значений степени точности, что позволит определить работоспособность вычислительного процесса. Для рассматриваемого примера можно использовать значения 
равные 0,01; 0,001; 0,0001.
Определение начальных условий осуществляется в соответствии с выбранным методом вычислений. Для рассматриваемого ряда одно из начальных условий универсально (Z = 0), а второе различно (i = 1 при расчёте напрямую, zi-1 = 1 при рекуррентном расчёте).
Технология вычисления степенных рядов (цепных дробей) представлена конкретной задачей (8.3).
Постановка задачи
Рассчитать значение функции ex при любом значении x. Расчёт производить разложением функции в степенной ряд до достижения заданной степени точности 
, 
, 
.
