Принципы формирования двумерных массивов из одномерных представлены конкретной задачей (9.2) о перевозках.
Постановка задачи
В городе имеется N продуктовых магазинов. Продукты поставляет одна база. Ассортимент (K) и масса (Mj) продуктов, поставляемых в каждый магазин, являются постоянными. Требуется рассчитать стоимость доставки каждого продукта в каждый магазин. Расстояния от базы до магазинов известны, а расходы на перевозку тонны продуктов на один километр составляют 1,30 р.
Формирование математической модели
Исходные данные
| N | [ед.] | – число магазинов; |
Si , 1  i i  N N
| [км] | – расстояния от базы до магазинов; |
| K | [ед.] | – количество продуктов в ассортименте; |
Mj , 1  j j  K K
| [т] | – массы продуктов в каждый магазин; |
| УР = _,_ _ | [р./(т  км)] км)]
| – удельные расходы на доставку. |
Расчётные зависимости
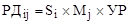
| [р. = км  т т   р./(т р./(т  км)]] км)]]
| – расходы на доставку в i-й магазин j-го продукта; |
1  i i  N, 1 N, 1  j j  K K
| – диапазоны изменения индексов; | |
| i = i + 1, j = j + 1 | – законы изменения индексов. |
Выбор метода решения
Математическая модель позволяет решить задачу двумя вариантами:
· осуществить расчёт затрат на доставку каждого продукта из ассортимента в один магазин, а затем повторить вычисления для всех оставшихся магазинов;
· рассчитать стоимость доставки одного продукта в каждый магазин, а затем повторить эти вычисления для всех остальных продуктов.
В первом варианте в качестве внутреннего цикла используется изменение массы каждого продукта, завозимого в i-й магазин (изменение параметра j), а в качестве внешнего – перебор магазинов, т. е. расстояний до них (параметр i). При вычислениях по второму варианту циклы поменяются местами.
Выбор варианта не влияет на результаты решения и позволяет в качестве метода решения использовать схему вычислений с одним последовательно вложенным циклом.
Составление алгоритма решения
Математическая формулировка и выбранный метод решения позволяют выполнить схему алгоритма (рис. 9.7).
Вывод результатов предполагается в форме таблицы, определяющей номер магазина, расстояние до него, номер продукта в ассортименте, его массу и расходы на доставку.
Программирование задачи
Планируемая алгоритмом методика вывода результатов (последовательностью переменных) позволяет рассчитываемые затраты на доставку обозначить как:
· элемент двумерного массива rd[i][j];
· неиндексированная переменная rdij.
Первый вариант обязателен при необходимости хранения и дальнейшего использования результатов счета. Он реализуется созданием дополнительного двумерного массива для хранения полученных значений. Второй применим, когда результаты счета не нуждаются в хранении.

Рис. 9.7. Схема алгоритма решения задачи о перевозках
Тогда их можно последовательно размещать в одной ячейке, как промежуточные значения (константы) одной простой переменной.
В рассматриваемой задаче не предполагается последующего использования значений РДij, поэтому в программе предусмотрен вывод этих значений в виде простой (неиндексированной) переменной rdij.
Идентификация переменных представлена в табл. 9.2.
Таблица 9.2
| Обозначение в алгоритме | N | K | УР | i | j | Si | Mj | РДij |
| Обозначение в программе | n | k | ur | i | j | s[i] | m[j] | rdij |
На основании схемы алгоритма и таблицы идентификации составим программы решения задачи.
Классический вариант программирования задачи (без элементов дружественности при выводе)
#include <stdio.h> /* директивы */
#include <conio.h> /* препроцессора */
#include <math.h>
#include <windows.h>
#define N 15 /* увеличенные */
#define K 10 /* размеры массивов */
main() /* заголовок головной функции */
{
float s[N], m[K], ur, rdij; /* описатели массивов */
int i, j, n, k; /* и переменных */
char buf[50]; /*описание символьного массива*/
clrscr();
CharToOem(" Введите число магазинов N ",buf); /* запрос */
printf("\n %s (N<=%d):",buf,N); /* и ввод */
scanf("%d", &n); /* фактических */
CharToOem(" Введите количество продуктов K ",buf);
printf("\n %s (K<=%d):",buf,K); /* размеров */
scanf("%d", &k); /* массивов */
CharToOem("Введите расходы на доставку УР (р./т км.):",buf);
printf("\n %s ",buf);
scanf("%f", &ur);
CharToOem("Расходы на доставку УР (р./т км.):",buf);
printf("\n N=%d K=%d %s =%.2f ", n, k, buf, ur);
for(i = 0; i < n; i++) /* заголовок цикла ввода s[i] */
{
CharToOem("Введите расстояние в км S ",buf);
printf("\n %s (%d):",buf,i+1);
scanf("%f", &s[i]);
}
for(i = 0; i < n; i++) /* заголовок цикла вывода s[i] */
printf(" %.2f", s[ i ]);
printf("\n"); /* перевод курсора в начало следующей строки */
for(j = 0; j < k; j++) /* заголовок цикла ввода m[j] */
{
CharToOem("Введите массу в тоннах М ",buf);
printf("\n %s (%d):",buf,j+1);
scanf("%f", &m[j]);
}
for(j = 0; j < k; j++) /* заголовок цикла вывода m[j] */
printf(" %.3f", m[ j ]);
printf("\n\n"); /* перевод курсора в начало следующей строки */
for(i = 0; i < n; i++) /*заголовок внешнего цикла расчета rdij*/
{
printf(" \n\n %5d \t %6.2f \n", i+1, s[ i ]);
for(j = 0; j < k; j++) /* заголовок внутр. цикла расчета rdij */
{
rdij = s[ i ] * m[ j ] * ur;
printf(" %2d %6.3f %9.2f\n ", j+1, m[j],rdij);
}
}
getch();
}
3 4 130.8
82 34.5 16.7
12.3 43. 25.15 64.5
Под закрывающей скобкой приведены исходные данные для решения задачи.
Результаты решения представлены в приложении 9.3.
Программирование задачи с графическим интерфейсом
Программирование задачи при использовании графического интерфейса предварим его разработкой.
Для ввода числа магазинов, количества продуктов, расходов на доставку планируем однострочные поля редактирования (EditN, EditK, EditUr). Для ввода расстояний до магазинов и масс доставляемых продуктов – многострочные поля редактирования (EditS, EditM). Вывод текущих значений исходных масс и расстояний реализуем в поля-списки (ListBoxM, ListBoxS). Рассчитываемые расходы на доставку – в поле-список (ListBoxRd) так, чтобы значения расходов размещались на пересечении соответствующих значений массы и расстояния.
|
|
|

Управление процессом решения реализуем двумя командными кнопками, расположенными в нижней части окна. Назначение каждой определяется ее названием.
С учетом планируемого интерфейса выполним программирование задачи.
#include<stdio.h>
#include<stdlib.h>
#include <string.h>
#define K 10 /* увеличенные */
#define N 15 /* размеры массивов */…
void TSumprDlgClient::Ok()
{
// INSERT>> Your code here.
float s[N], m[K], ur, rdij; /* описатели массивов */
int i, j, n, k; /* и переменных */
char buf[10],buf1[30] = “ ”; /*описание символьного массива*/
ListBoxRd->ClearList();/*очистка поля вывода*/
ListBoxS->ClearList();/*очистка поля вывода*/
ListBoxM->ClearList();/*очистка поля вывода*/
EditN->GetText(buf, 10); /*ввод количества*/
n = atoi(buf); /* магазинов*/
EditK->GetText(buf, 10); /*ввод количества*/
k = atoi(buf); /* продуктов*/
EditUR->GetText(buf, 10); /*ввод расходов*/
ur = atof(buf); /* на доставку */
for(i = 0; i < n; i++) /* заголовок цикла ввода s[i] */
{
EditS->GetLine(buf, 10, i); /* ввод элементов */
s[i]=atof(buf); /* массива S*/
}
for(i = 0; i < n; i++) /* заголовок цикла вывода s[i] */
{ sprintf(buf,"%8.2f",s[i]); /* вывод текущих*/
ListBoxS->AddString(buf); /*значений si*/
}
for(j = 0; j < k; j++) /* заголовок цикла ввода m[j] */
{
EditM->GetLine(buf, 10, j); /* ввод элементов */
m[j]=atof(buf); /* массива M*/
}
for(j = 0; j < k; j++) /* заголовок цикла вывода m[j] */
{
sprintf(buf," %8.2f ",m[j]); /* вывод текущих */
strcat(buf1, buf); /* склеенных*/
}
ListBoxM->AddString(buf1); /*значений mi*/
for(i = 0; i < n; i++) /*заголовок внешнего цикла расчета rdij*/
{
sprintf(buf1,"%s","");
for(j = 0; j < k; j++) /* заголовок внутр. цикла расчета rdij */
{
rdij = s[ i ] * m[ j ] * ur;
sprintf(buf," %8.2f ",rdij); /* вывод текущих */
strcat(buf1, buf); /* склеенных */
}
ListBoxRd->AddString(buf1); /*значений rdij*/
}
}
3 4 130.8
82 34.5 16.7
12.3 43. 25.15 64.5
Под закрывающей скобкой приведены исходные данные для решения задачи.
Описатели вводимых массивов показывают, что количество магазинов максимально может быть равно пятнадцати, а ассортимент включать до десяти наименований.
В запросах на ввод текущих значений расстояний и масс и при выводе таблицы результатов индексы магазина и продукта увеличены на единицу. Это позволяет перейти от принятой в Си/Си++ формы обозначения индексов (от 0) к принятой в математике (от 1).
Результаты решения представлены в приложении 9.4.






