Ранжирование символьных массивов

Особенность цифровых вычислительных машин определяет представление любой нечисловой информации (буквы алфавитов, знаки) конкретными цифровыми комбинациями – кодами.

В кодовой таблице ASCII ANSI символы обозначаются десятичными триадами от 000 до 255. Традиционное расположение их в таблице – по возрастанию кодов:

· специальные символы;

· цифры;

· прописные буквы латинского алфавита (A – Z);

· строчные буквы латинского алфавита (a – z);

· прописные буквы русского алфавита (А – Я);

· строчные буквы русского алфавита (а – я).

Следовательно, первая буква конкретного алфавита имеет наименьший код из всех последующих, а последняя – наибольший. Коды прописных букв меньше, чем строчных, латинских – меньше русских. Это позволяет организовать сравнение и перебор символьной информации (их кодов) не только по каждой из позиций, но и их совокупностей.

Принципиально возможно ранжирование символьной информации в двух вариантах (рис. 9.15).

Рис. 9.15. Варианты ранжирования символьной информации

Детализировано ранжирование символьных массивов представлено ниже.

Ранжирование символов в строке по алфавиту

В качестве метода поиска используем модифицированное «всплывание пузырька». Общая идея метода – непосредственное циклического сравнение кодов первого из элементов массива с кодами всех последующих. Если код текущего элемента меньше кода первого, то они меняются местами. Результат первого цикла сравнения – «всплывший» символ с минимальным кодовым значением (одна из начальных букв алфавита), позволяет уменьшить сортируемый массив на единицу (без первого отсортированного элемента), а затем повторять общую идею на сформированном предыдущим шагом укороченном массиве.

Упорядочение символов в строке по алфавиту рассмотрим на конкретной задаче (9.6) о символьной строке.

Постановка задачи

Дан одномерный символьный массив строчных букв кириллицы (строка) максимальным размером 30 элементов. Требуется упорядочить исходную строку по алфавиту.

Формирование математической модели

Исходные данные

BUF(N) – символьный массив;

N £ 30 – максимальный размер массива;

n – реальный размер массива (длина строки).

Модель массива BUF(n):

buf₁

buf₂

...

buf_i

...

buf_n

i – текущий индекс массива;

i = i + 1 – закон изменения индекса;

1 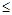i 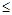n – диапазон изменения номера i элемента.

Расчётные зависимости

buf_min₁ = min(buf₁, buf₂,…, buf_i,…, buf_n);

buf₁ = buf_min1;

buf_min2 = min(buf₂,…, buf_i,…, buf_n);

buf₂ = buf_min2;

…

buf_{min i} = min(buf_i,…, buf_n-1, buf_n);

buf_i = buf_{min i};

…

buf_{min n-1} = min(buf_n-1,buf_n);

buf_n-1 = buf_{min n-1};

Выбор метода решения

Решение задачи выполним модифицированным методом «пузырька». Он реализуется последовательностью:

· присвоить индексу внешнего цикла его начальное значение (i = 1) – зафиксировать номер i элемента buf_i, с которым идет сравнение;

· присвоить индексу внутреннего цикла его начальное значение через внешний (j = i+1);

· сравнить зафиксированное значение buf_i с текущим buf_j (buf_i > buf_j);

· выполнить переприсваивание bufпр = buf_i, buf_i = buf_j и buf_j = bufпр, если условие выполняется;

· изменить индекс внутреннего цикла по закону j = j + 1;

· повторять три предыдущих пункта пока j £ n;

· изменить индекс внешнего цикла по закону i = i + 1;

· повторять предыдущие пункты, кроме первого, пока i £ n-1;

· прекратить решение при i > n-1.

Следовательно, в качестве метода решения необходимо выбрать структуру последовательно вложенных циклов арифметического типа с аналитическим изменением аргумента, внутренний из которых – смешанный вычислительный процесс (цикл с расположенным внутри него ветвлением) для перемещения минимального значения элементов в начало массива последовательно уменьшающейся длины.