Последовательно вложенные циклы

Типовое использование последовательно вложенных циклов – обработка многомерных массивов (задач, в которых они используются) и преобразования одномерных массивов (сортировка элементов).

Варианты использования (функционального назначения) вложенных циклов представлены на рис. 9.2.

Рис. 9.2. Функциональное назначение вложенных циклов

Обработка элементов многомерных массивов

Рассмотрим обработку многомерных массивов на конкретной задаче (9.1) о расчете элементов двумерного массива.

Постановка задачи

Имеется двумерный массив X размером (m n). Рассчитать аналогичный ему массив Y(m n), каждый элемент которого равен частному от деления соответствующего элемента массива X на два.

Формирование математической модели

Исходные данные

m – размер, определяющий число строк матрицы X ();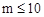

n – размер, определяющий число столбцов матрицы X ().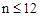

Модель матрицы X(m n):

x11	x12	...	x1j	...	x1n
x21	x22	...	x2j	...	x2n
...	...	...	...	...	...
xi1	xi2	...	xij	...	xin
...	...	...	...	...	...
xm1	xm2	...	xmj	...	xmn

1 i m – диапазон изменения номера i строки;

1 j n – диапазон изменения номера j столбца.

Расчётные зависимости

Вычисление текущего элемента искомой матрицы Y:

, для всех 1 i m и 1 j n

Модель матрицы Y(m n):

y11	y12	...	y1j	...	y1n
y21	y22	...	y2j	...	y2n
...	...	...	...	...	...
yi1	yi2	...	yij	...	yin
...	...	...	...	...	...
ym1	ym2	...	ymj	...	ymn

Выбор метода решения

Решение задачи можно осуществить двумя вариантами. Первый реализуется последовательностью:

· присвоить индексу строки его начальное значение (i = 1);

· присвоить индексу столбца его начальное значение (j = 1);

· рассчитать искомое , сохранив его в соответствующей ячейке;

· изменить индекс столбца по закону j = j + 1;

· повторять два предыдущих пункта пока j £ n;

· изменить индекс строки по закону i = i + 1;

· повторять пять предыдущих пунктов пока i £ m;

· прекратить решение при i > m.

Второй вариант реализации:

· присвоить индексу столбца его начальное значение (j = 1);

· присвоить индексу строки его начальное значение (i = 1);

· рассчитать искомое , сохранив его в соответствующей ячейке;

· изменить индекс строки по закону i = i + 1;

· повторять два предыдущих пункта пока i £ m;

· изменить индекс столбца по закону j = j + 1;

· повторять пять предыдущих пунктов пока j £ n;

· прекратить решение при j > n.

С точки зрения результатов методы идентичны, поэтому, выбрав для реализации первый, детализируем его. Присвоив индексу строки начальное значение i = 1, и, изменяя индекс столбца j от 1 до n с шагом 1, выберем каждый из элементов x_1j и, разделив его на 2, получим соответствующие элементы y_1j первой строки искомого массива Y. Повторим вычисления для каждой из следующих строк, индексы которых изменяются от 1 до m с шагом 1.

Следовательно, анализ математической модели позволяет сделать вывод, что решение требует использования структуры с одним последовательно вложенным циклом. При этом в качестве внешнего цикла принят перебор строк (индекс i), а в качестве внутреннего – перебор столбцов (индекс j).

При вычислениях по второму варианту циклы поменяются местами.