Исходные данные
X(N) – целочисленный массив;
N £ 30 – максимальный размер массива;
n – реальный размер массива.
Модель массива Х(n):
| х1 | х2 | ... | хi | ... | хn |
i – текущий индекс массива;
i = i + 1 – закон изменения индекса;
1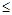 
i 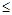n – диапазон изменения номера i элемента.
Расчётные зависимости
xmax1 = max(x1, x2,…, xi,…, xn);
x1 = xmax1;
xmax2 = max(x2,…, xi,…, xn);
x2 = xmax2;
…
xmax i = max(xi,…, xn-1, xn);
xi = xmax i;
…
xmax n-1 = max(xn-1,xn);
xn-1 = xmax n-1;
Выбор метода решения
Анализ математической модели определяет необходимость использования структуры «вложенные циклы». Внешний цикл необходим для формирования текущих массивов, начиная с исходного, с последовательно уменьшающимся количеством элементов (от N-1 вначале до N < 2 в конце). Поиск экстремального значения в каждом текущем массиве требует внутреннего смешанного вычислительного процесса (цикла с вложенным ветвлением). Таким образом, метод решения реализуется последовательностью:
· присвоить индексу внешнего цикла его начальное значение (i = 1);
· сформировать начальные максимальные значения искомого х max и номера ячейки n max, где он хранится;
· присвоить индексу внутреннего цикла его начальное значение через внешний (j = i + 1);
· проверить текущее значение xj на текущее максимальное (xj > xmax);
· выполнить переприсваивание xmax = xj и nmax = j, если условие выполняется;
· изменить индекс внутреннего цикла по закону j = j + 1;
· повторять три предыдущих пункта пока j £ n;
· выполнить переприсваивание xn max = xi и xi = xmax,
· изменить индекс внешнего цикла по закону i = i + 1;
· повторять предыдущие пункты, кроме первого, пока i £ n-1;
· прекратить решение при i > n-1.
Следовательно, в качестве метода решения необходимо выбрать структуру последовательно вложенных циклов арифметического типа с аналитическим изменением аргумента, внутренний из которых смешанный вычислительный процесс – цикл с расположенным внутри него ветвлением поиска максимального значения функции и перестановки в начало массива последовательно уменьшающейся длины.
Составление алгоритма решения
Математическая формулировка задачи и выбранный детализированный метод ее решения позволяют создать одношаговую схему алгоритма решения (рис. 9.13). Ввод и вывод исходного и получаемого массивов предусмотрен отдельно сформированными циклами.
Рис. 9.13. Схема алгоритма сортировки элементов одномерного числового массива по убыванию
Программирование задачи
Таблица идентификации переменных алгоритма и создаваемой программы представлена в табл. 9.4.
Таблица 9.4
| Имя в алгоритме | n | i | j | xmax | xj | xi | xnmax | nmax |
| Имя в программе | n | i | j | xmax | x[j] | x[i] | x[nmax] | nmax |
На основании схема алгоритма и таблицы идентификации составим программы решения задачи.
Классический вариант программирования задачи
#include<stdio.h>
#include<stdlib.h>
#include<windows.h>
#include<conio.h>
main()
{
int x[30], xmax; /* описание */
int i, j, n, nmax; /* локальных переменных */
char buf[50]; /*описание символьного массива*/
clrscr();
CharToOem("Введите количество элементов массива", buf);
printf("\n %s \n",buf); /* ввод*/
scanf("%d", &n);
for(i=0; i < n; i++)
{
CharToOem(" Введите элемент x ",buf);
printf("\n %s[%d] \n",buf,i+1); /* ввод*/
scanf("%d", &x[i]);
}
CharToOem(" \n\n Исходный массив X \n\n",buf);
printf("%s",buf);
for(i=0;i<n;i++)
printf(" %5d ",x[i]);
for (i = 0; i < n; i++)/*заголовок внешн. цикла сортировки*/
{
xmax = x[i];
nmax = i;
for(j = i+1; j < n; j++) /*загол. внутр. цикла сортировки*/
{
if(x[j] > xmax)
{
xmax = x[j];
nmax = j;
}
}
x[nmax] = x[i];
x[i]=xmax;
}
CharToOem(" \n Отсортированный массив Х \n",buf);
printf("%s",buf);
for(i=0;i<n;i++) printf(" %5d ",x[i]);
getch();
}
7 – размер массива;
1 6 4 8 2 11 4 – элементы массива;
Под закрывающей скобкой приведены исходные данные для решения задачи.
Результаты решения представлены в приложении 9.7.
Программирование задачи с графическим интерфейсом
Программирование задачи при использовании графического интерфейса предварим его разработкой.
|
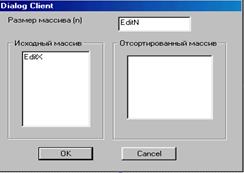
Для ввода количества элементов массива планируем однострочное поле редактирования (EditN). Для ввода элементов массива Х – многострочное поле редактирования (EditХ). Вывод элементов отсортированного массива X реализуем в поле-список (ListBoxX).
Управление процессом решения реализуем двумя командными кнопками, расположенными в нижней части окна. Назначение каждой определяется ее названием.
С учетом планируемого интерфейса выполним программирование задачи.
#include<stdio.h>
#include<stdlib.h>
…
void TVrDlgClient::BNClickedOk()
{
// INSERT>> Your code here.
int x[30], xmax; /* описание */
int i, j, n, nmax; /* локальных переменных */
char buf[50]; /*описание символьного массива*/
ListBoxX->ClearList();
EditN->GetText(buf,10);/*Ввод размера*/
n=atoi(buf); /*массива */
for(i=0; i < n; i++)
{
EditX->GetLine(buf,10,i); /* ввод*/
x[i]=atoi(buf); /* текущего элемента массива*/
}
for (i = 0; i < n; i++)/*заголовок внешн. цикла сортировки*/
{
xmax = x[i];
nmax = i;
for(j = i+1; j < n; j++) /*загол. внутр. цикла сортировки*/
{
if(x[j] > xmax)
{
xmax = x[j];
nmax = j;
}
}
x[nmax] = x[i];
x[i]=xmax;
}
for (i=0; i< n; i++)/* заголовок цикла вывода */
{
sprintf(buf," %3d",x[i]); /* вывод*/
ListBoxX->AddString(buf); /* элемента массива*/
}
}
7 – размеры массива;
1 6 4 8 2 11 4 – элементы массива;
Под закрывающей скобкой приведены исходные данные для решения задачи.
Результаты решения представлены в приложении 9.8.
9.3.1.2. Ранжирование по возрастанию методом «пузырька»
Рассмотрим ранжирование по возрастанию на конкретной задаче (9.5) о числовом одномерном массиве А. В качестве метода поиска используем «всплывание пузырька».
Постановка задачи
Дан одномерный вещественный массив А максимально содержащий до 20 элементов. Диапазон представления численных значений элементов от -50 до 50. Требуется отранжировать исходный массив по возрастанию. Предусмотреть возможность прекращения ввода элементов массива (не более 20) по желанию пользователя.
