Дифференциалом функции у=ƒ(х) в точке х называется главная часть ее приращения, равная произведению производной функции на приращение аргумента, и обозначается dу (или dƒ(х)): dy=ƒ'(х)•∆х.
Основные дифференциалы:
Дифференциал функции обладает свойствами, аналогичными свойствам производной.
- Дифференциал постоянной равен нулю:
dc = 0, с = const. - Дифференциал суммы дифференцируемых функций равен сумме дифференциалов слагаемых:
d(u+v)=du + dv
Следствие. Если две дифференцируемые функции отличаются постоянным слагаемым, то их дифференциалы равны
d(u+c) = du (c= const).
- Дифференциал произведения двух дифференцируемых функций равен произведению первой функции на дифференциал второй плюс произведение второй на дифференциал первой:
d(uv) = udv + vdu.
Следствие. Постоянный множитель можно выносить за знак дифференциала
d(cu) = cdu (с = const).
- Дифференциал частного u/v двух дифференцируемых функций и = и(х) и v = v(x) определяется формулой
- Свойство независимости вида дифференциала от выбора независимой переменной (инвариантность формы дифференциала): дифференциал функции равен произведению производной на дифференциал аргумента независимого от того, является ли этот аргумент независимой переменной или функцией другой независимой переменной.
Производные и дифференциалы высших порядков.
Пусть производная некоторой функции f дифференцируема. Тогда производная от производной этой функции называется второй производной функции f и обозначается f". Таким образом,
f" (x) = (f' (x)) '.
Если дифференцируема (n - 1)-я производная функции f, то ее n -й производной называется производная от (n - 1)-й производной функции f и обозначается f(n). Итак,
f(n) (x) = (f(n-1) (x)) ', n ϵ N, f(0) (x) = f (x).
Число n называется порядком производной.
Дифференциалом n -го порядка функции f называется дифференциал от дифференциала (n - 1)-го порядка этой же функции. Таким образом,
dnf (x) = d (dn -1 f (x)), d 0 f (x) = f (x), n ϵ N.
Если x - независимая переменная, то
dx = const и d 2 x = d 3 x =... = dnx = 0.
В этом случае справедлива формула
dnf (x) = f (n)(x)(dx) n.
Производные n -го порядка от основных элементарных функций
Справедливы формулы
Применение производных к исследованию функций.
Основные теоремы дифференцирования функций:
Теорема Ролля
Пусть функция f: [ a, b ] → R непрерывна на сегменте [ a, b ], и имеет конечную или бесконечную производную внутри этого сегмента. Пусть, кроме того, f (a) = f (b). Тогда внутри сегмента [ a, b ] найдется точка ξ такая, что f' (ξ) = 0.
Теорема Лагранжа
Если функция f: [ a, b ] → R непрерывна на сегменте [ a, b ] и имеет конечную или бесконечную производную во внутренних точках этого сегмента, то 
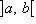такое, что f (b) - f (a) = f' (ξ)(b - a).
Теорема Коши
Если каждая из функций f и g непрерывна на [ a, b ] и имеет конечную или бесконечную производную на ] a, b [ и если, кроме того, производная g' (x) ≠ 0 на ] a, b [, то 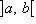такое, что справедлива формула
Если дополнительно потребовать, чтобы g (a) ≠ g (b), то условие g' (x) ≠ 0 можно заменить менее жестким:
