Предел произведения нескольких функций равен произведению пределов этих функций:
5) Предел частного
Предел частного двух функций равен отношению пределов этих функций при условии, что предел знаменателя не равен нулю:
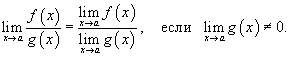
Односторонние пределы
Пусть на некотором числовом множестве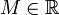 
задана числовая функция 
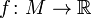и число 
— предельная точка области определения 
.
7. Замечательные пределы. Виды неопределённостей и как они раскрываются.
1) 
=1 -> 
2) y=f(x) ->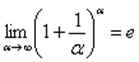 
Выше предоставлены 2 замечательных предела!!!
Виды неопределённостей и как они раскрываются
Бесконечно малые и бесконечно большие функции. Таблица эквивалентностей.
· Y=f(x) def бесконечно малой при x->x0, если lim f(x) = 0!
Пример: lim x-> 1 (x^3-1) = 0 => x^3-1 – б.м.ф при x ->1
· Y=f(x) def бесконечно большой при x->x0, если lim x->x0 f(x) = 
∞!!!
Пример: lim x-> 0 1/x = ∞ => 1/x -> б.б.ф
Если a(x) и 
– б.м.ф, то a(x)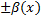 
– б.м.ф, аналогично с перемножением и умножением на const!
Сравнение б.м.ф и б.б.ф
· a(x), b(x) – б.м.ф, то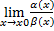 
= const тогда a(x) и b(x) одного порядка малости.
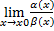· =0 тогда a(x) – бесконечно малая более высокого порядка.
· Если lim = ∞ тогда b(x) – бесконечно малая более высокого порядка.
· Если lim =1 – тогда a(x) и b(x) эквивалентны.
Таблица эквивалентностей:
Непрерывность функций. Точки разрыва.
f(x) def непрерывной в точке x0, если:
Ø она определена функцией
Ø односторонние пределы существуют и равны + равны значения функций в этой точке.
Функция непрерывна на промежутке, если она не прерывна в каждой точке этой f(x)!
Если все условия не выполняются – в этой точке нет непрерывности!
1) lim x-> x0-0 f(x) ≠lim x0=->x0+0 f(x) -> тогда x0 – точка разрыва первого рода.
2) Если хотя бы один из одностороннего предела не существует, тогда x0 – точка разрыва второго рода. + x=x0 – асинтода. F(x) = 1/x
3) Оба предела существуют и равны между собой. Lim x->x-0 f(x) = lim x-> x+0 f(x), тогда x0 – точка устранимого разрыва.
Локальные свойства непрерывных функций.
Л.Ф – наз. такие свойства ф-ий, кот опред. поведение ф-ии в сколько угодно малой окрестности в любой точке определения.
1 Теорема – если y=f(x) непрерывна в точке x0, то она обязательно ограничена в какой т окрестности этой точки.
2 Теорема – если y=f(x) непрерывна в точке x0 и y(x0) ≠0, то некоторой окрестност этой точки x0 все значения ф-ии либо + либо -!!!
3. Теорема – f(x) + g(x) – если эти 2 функции непрерывны в точке x0,значит в этой точке непрерывна их сумма(разность, произведение и т.д)
4 Теорема – если -U=U(x) имеет предел в точке x0 равный A, то ф-ия y=f(U(x)) непрерывна. Lim 
= 
5 Теорема (непрерывность сложной ф-ии) – если U=U(x) непрерывна в точке x0, а y=f(U) непрерывна в точке U0, тогда тогда сложная ф-ия y=f(U(x)) также будет непрерывна в точке x0.
