Множества и операции над ними. Свойства операций.
Множества – это совокупность элементов, объединённых общими свойствами.
Принадлежность элемента множеству:
· 
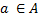– принадлежность элемента a к множеству A
· a ₵ A – непринадлежность элемента a к мноеству A
· A U B – объединение множеств, или множество С с элементами множеств A и B
· 
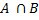- пересечение множеств, или множество С с общими элементами A и В
· A \ B – разность двух множеств, или множество C, которое состоит из элементов множества A, которых нет в множестве B.
· 
– симметрическая разность двух множеств, или множество C, которое состоит из не общих элементов множеств A и B.
· СuA = Ā – дополнение множества, или множество A является множеством U, тогда определяется операция дополнения - СuA = Ā = U\A
· A C B – вхождение одного множества в другое множество, или если любой элемент множества A является элементом множества B, то говорят, что множество A есть подмножество множества B (множество A входит в множество B).
· A ₵ B - Не вхождение одного множества в другое множество, или если существует элемент множества A, который не является элементом множества B, то говорят, что множество A не подмножество множества B.
Свойства операций над множествами.
Множества вещественных чисел. Свойства операций над ними и геометрическая интерпретация.
Вещественное число - это любое положительное число, отрицательное число или нуль.
· Вещественные числа можно складывать, и при этом выполняются следующие законы:
(коммутативный) 
(ассоциативный)
(существование нуля)
= 0 (существование противоположного элемента)
- 
· Вещественные числа можно перемножать, и при этом выполняются следующие законы:
(коммутативный)
(ассоциативный)
(существование единицы)
Приме: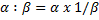 
и 
· Каждое вещественное число, отличное от нуля, либо положительно, либо отрицательно. При этом сумма и произведение положительных чисел — положительное числа.
· Каждое вещественное число, отличное от нуля, либо положительно, либо отрицательно. При этом сумма и произведение положительных чисел — положительное числа.
Геометрическая интерпретация вещественных чисел: каждой точке числовой оси 0x ставится в соответствие вещественное число x, и обратно, каждому вещественному числу x соответствует единственная точка числовой оси.
Функции. Определение и общие свойства.
Функция - зависимость переменной у от переменной x, если каждому значению х соответствует единственное значение у. Переменную х называют независимой переменной или аргументом. Переменную у называют зависимой переменной.
Графиком функции называют множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты - соответствующим значениям функции.
Свойста:
1) Область определения функции и область значений функции.
(I) Область определения функции - это множество всех допустимых действительных значений аргумента x (переменной x), при которых функция y = f(x) определена.
(II) Область значений функции - это множество всех действительных значений y, которые принимает функция.
(III) Нули функции. Нуль функции – такое значение аргумента, при котором значение функции равно нулю.
(IV) Промежутки знакопостоянства функции. Промежутки функции – такие множества значений аргумента, на которых значения функции только положительны или только отрицательны.
(V) Монотонность функции. Возрастающая функция. Убывающая функция.
(VI) Чётность (нечётность) функции. Чётная функция - функция, у которой область определения симметрична относительно начала координат. График чётной функции симметричен относительно оси ординат. Нечётная функция - функция, у которой область определения симметрична относительно начала координат. График нечётной функции симметричен относительно начала координат.
(VII) Ограниченность функции. Функция называется ограниченной, если существует такое положительное число M, что |f(x)| ≤ M для всех значений x. Если такого числа не существует, то функция - неограниченная.
(VIII) Периодическость функции. Функция f(x) - периодическая, если существует такое отличное от нуля число T, что для любого x из области определения функции имеет место: f(x+T) = f(x). Такое наименьшее число называется периодом функции. Все тригонометрические функции являются периодическими.
