Кинетический момент механической системы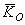 
относительно неподвижного центра O является мерой движения системы вокруг этого центра. При решении задач обычно применятся не сам вектор 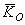, а его проекции на оси неподвижной системы координат, которые называются кинетическими моментами относительно оси. Например, 
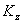- кинетический момент системы относительно неподвижной оси Oz.
Кинетический момент механической системы складывается из кинетических моментов точек и тел, входящих в эту систему. Рассмотрим способы определения кинетического момента материальной точки и твердого тела при различных случаях их движения.
Для материальной точки с массой 
, имеющей скорость 
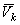, кинетический момент относительно некоторой оси Oz определяется как момент вектора количества движения этой точки относительно выбранной оси:
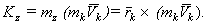
Кинетический момент точки считается положительным, если со стороны положительного направления оси движение точки происходит против часовой стрелки.
Если точка совершает сложное движение, для определения ее кинетического момента следует вектор количества движения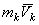 
рассматривать как сумму количеств относительного и переносного движений (рис.41)
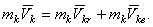
Тогда
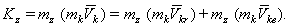
Но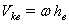 
, где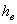 
- расстояние от точки до оси вращения, и
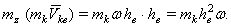
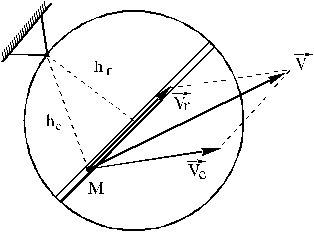
Рис. 41
Вторую составляющую вектора кинетического момента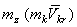 
можно определить так же, как и момент силы относительно оси. Как и для момента силы, величина 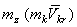равна нулю, если вектор относительной скорости лежит в одной плоскости с осью переносного вращения.
Кинетический момент твердого тела относительно неподвижного центра можно определить как сумму двух составляющих: первая из них характеризует поступательную часть движения тела вместе с его центром масс, вторая - движение системы вокруг центра масс:
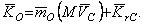
Если тело совершает поступательное движение, то вторая составляющая равна нулю
.
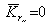Наиболее просто вычисляется кинетической момент твердого тела при его вращении вокруг неподвижной оси
,
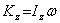где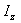 
- момент инерции тела относительно оси вращения.
Теорема об изменении кинетического момента механической системы при ее движении вокруг неподвижного центра формулируется следующим образом: полная производная по времени от вектора кинетического момента механической системы относительно некоторого неподвижного центра O по величине и направлению равна главному моменту внешних сил, приложенных к механической системе, определенному относительно того же центра
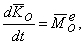
где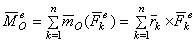 
- главный момент всех внешних сил относительно центра О.
При решении задач, в которых рассматриваются тела, вращающиеся вокруг неподвижной оси, используют теорему об изменении кинетического момента относительно неподвижной оси
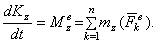
Как и для теоремы о движении центра масс, теорема об изменении кинетического момента имеет следствия.
Следствие 1. Если главный момент всех внешних сил относительно некоторого неподвижного центра равен нулю, то кинетический момент механической системы относительно этого центра остается неизменным.
Следствие 2. Если главный момент всех внешних сил относительно некоторой неподвижной оси равен нулю, то кинетический момент механической системы относительно этой оси остается неизменным.
Теорема об изменении кинетического момента применяется для решения задач, в которых рассматривается движение механической системы, состоящей из центрального тела, вращающегося вокруг неподвижной оси, и одного или нескольких тел, движение которых связано с центральным.. Связь может осуществляться при помощи нитей, тела могут перемещаться по поверхности центрального тела или в его каналах за счет внутренних сил. С помощью данной теоремы можно определить зависимость закона вращения центрального тела от положения или движения остальных тел.
Пример 12. Рассмотрим применение теоремы об изменении кинетического момента для определения внешнего момента, обеспечивающего равномерное движение ведущего звена механической системы. Механическая система (рис.42) состоит из однородной трубки CD длиной L, массы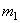 
, образующей с осью вращения прямой угол и шарика массы 
.
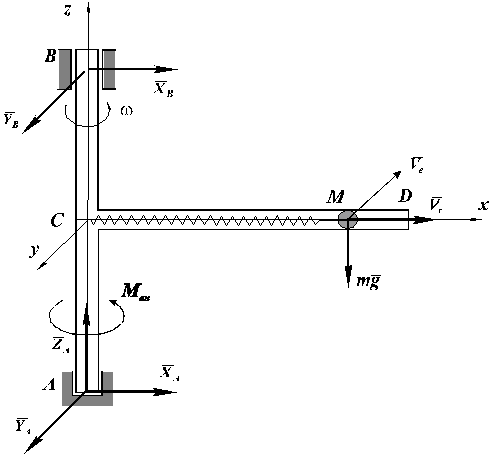
Рис.42
В момент времени t =0 под действием внешнего момента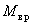 
трубка начинает вращаться вокруг вертикальной оси с постоянной угловой скоростью 
. Необходимо определить, каким должен быть этот момент, чтобы сохранялась постоянная угловая скорость вращения трубки CD. При решении пренебречь трением, массой стержня АВ и пружины.
Применим теорему об изменении кинетического момента, выбрав за ось z ось вращения АВ,
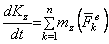. (9)
Определим кинетический момент рассматриваемой системы относительно оси Az. Трубка (однородный прямолинейный стержень) совершает вращение вокруг оси, перпендикулярной стержню и проходящей через его конец, имеет кинетический момент
,
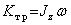где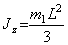 
- осевой момент инерции трубки,
- угловая скорость вращения.
Шарик М совершает сложное движение - относительное вдоль трубки со скоростью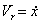 
и переносное вместе с трубкой. Переносная скорость 
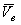перпендикулярна трубке и по модулю равна 
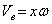. При определении переносной скорости за начало отсчета координаты x принята точка С трубки, лежащая на оси вращения. Кинетический момент шарика относительно оси z равен 
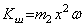, т.к. вектор 
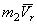пересекает ось z и его момент относительно этой оси равен нулю.
Кинетический момент всей системы равен
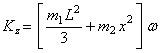. (10)
Определим главный момент внешних сил относительно оси z. Силы тяжести трубки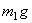 
и шарика 
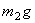параллельны оси вращения и момента относительно этой оси не создают. Реакции опор 
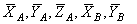пересекают ось вращения и момент этих сил относительно оси z также равен нулю. Силы динамического взаимодействия между шариком и трубкой, включая упругую силу пружины 
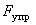, есть силы внутренние. Поэтому
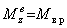, (11)
где 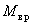- внешний момент, обеспечивающий равномерное вращение трубки.
Подставляя (8) и (9) в уравнение теоремы об изменении кинетического момента системы (7), получаем:
,
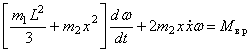откуда следует, что искомый внешний момент, обеспечивающий равномерное вращение трубки должен быть равен
.
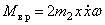Если в полученное соотношение подставить численные значения координаты x и относительной скорости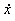 
, которые были получены в первом разделе курсовой работы, можно найти значение вращающего момента для любого момента времени и построить график изменения 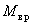на исследуемом интервале времени.
