Рассмотрим систему, вращающуюся вокруг неподвижной (или проходящей через центр масс) оси Оz. Тогда  . Если в этом случае
. Если в этом случае 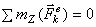 , то
, то

Отсюда приходим к следующим выводам.
а) Если система неизменяема (абсолютно твердое тело), то 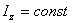 и, следовательно,
и, следовательно,  , т. е. твердое тело, закрепленное на оси, вращается в этом случае с постоянной угловой скоростью.
, т. е. твердое тело, закрепленное на оси, вращается в этом случае с постоянной угловой скоростью.
б) Если система изменяема, то под действием внутренних (или внешних) сил отдельные ее точки могут удаляться от оси, что вызывает увеличение  , или приближаться к оси, что приведет к уменьшению
, или приближаться к оси, что приведет к уменьшению  . Но поскольку
. Но поскольку  , то при увеличении момента инерции угловая скорость системы будет уменьшаться, а при уменьшении момента инерции - увеличиваться. Таким образом, действием внутренних сил можно изменить угловую скорость вращения системы, так как постоянство Кz не означает вообще постоянства
, то при увеличении момента инерции угловая скорость системы будет уменьшаться, а при уменьшении момента инерции - увеличиваться. Таким образом, действием внутренних сил можно изменить угловую скорость вращения системы, так как постоянство Кz не означает вообще постоянства  .
.
Рассмотрим некоторые примеры:
а) Опыты с платформой Жуковского. Для демонстрации закона сохранения момента количеств движения удобно пользоваться простым прибором, называемым «платформой Жуковского». Это круглая горизонтальная платформа на шариковых опорных подшипниках, которая может с малым трением вращаться вокруг вертикальной оси z. Для человека, стоящего на такой платформе,

и, следовательно,  . Если человек, разведя руки в стороны, сообщит себе толчком вращение вокруг вертикальной оси, а затем опустит руки, то величина
. Если человек, разведя руки в стороны, сообщит себе толчком вращение вокруг вертикальной оси, а затем опустит руки, то величина  уменьшится и, следовательно, угловая скорость вращения возрастет. Таким способом увеличения угловой скорости вращения широко пользуются в балете, при прыжках в воздухе (сальто) и т. п.
уменьшится и, следовательно, угловая скорость вращения возрастет. Таким способом увеличения угловой скорости вращения широко пользуются в балете, при прыжках в воздухе (сальто) и т. п.
Далее, человек, стоящий на платформе неподвижно (Кz=0), может повернуться в любую сторону, вращая вытянутую горизонтально руку в противоположном направлении. Угловая скорость вращения человека при этом будет такой, чтобы в сумме величина К z системы осталась равной нулю.
б) Раскачивание качелей. Давлением ног (сила внутренняя) человек, стоящий на качелях, раскачать их не может. Сделать это можно следующим образом. Когда качели находятся в левом верхнем положении A 0, человек приседает. При прохождении через вертикаль он быстро выпрямляется. Тогда массы приближаются к оси вращения z, величина  уменьшается, и угловая скорость
уменьшается, и угловая скорость  скачком возрастает. Это увеличение
скачком возрастает. Это увеличение  приводит в конечном счете к тому, что качели поднимутся выше начального уровня A 0. В правом верхнем положении, когда
приводит в конечном счете к тому, что качели поднимутся выше начального уровня A 0. В правом верхнем положении, когда  , человек опять приседает (на величине
, человек опять приседает (на величине  это, очевидно, не скажется); при прохождении через вертикаль он снова выпрямляется и т.д. В результате размахи качелей будут возрастать.
это, очевидно, не скажется); при прохождении через вертикаль он снова выпрямляется и т.д. В результате размахи качелей будут возрастать.
в) Реактивный момент винта. Воздушный винт, установленный на вертолете, не только отбрасывает воздух вниз, но и сообщает отбрасываемой массе вращение. Суммарный момент количеств движения отбрасываемой массы воздуха и вертолета должен при этом остаться равным нулю, так как система вначале была неподвижна, а силы взаимодействия между винтом и средой внутренние. Поэтому вертолет начинает вращаться в сторону, противоположную направлению вращения винта. Действующий при этом на вертолет вращающий момент называют реактивным моментом.
Чтобы предотвратить реактивное вращение корпуса одновинтового вертолета, на его хвостовой части устанавливают соответствующий рулевой винт. У многовинтового вертолета винты делают вращающимися в разные стороны.






