Обратные тригонометрические функции (арксинус, арккосинус, арктангенс и арккотангенс) являются основным элементарным функциями. Часто из-за приставки "арк" обратные тригонометрические функции называют аркфункциями. Сейчас мы рассмотрим их графики и перечислим свойства.
Функция арксинус y = arcsin(x).
Изобразим график функции арксинус:

Свойства функции арксинус y = arcsin(x).
· Областью определения функции арксинус является интервал от минус единицы до единицы включительно: 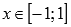 .
.
· Область значений функции y = arcsin(x):  .
.
· Функция арксинус - нечетная, так как 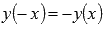 .
.
· Функция y = arcsin(x) возрастает на всей области определения, то есть, при 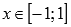 .
.
· Функция вогнутая при  , выпуклая при
, выпуклая при  .
.
· Точка перегиба (0; 0), она же ноль функции.
· Асимптот нет.
Функция арккосинус y = arccos(x).
График функции арккосинус имеет вид:

Свойства функции арккосинус y = arccos(x).
· Область определения функции арккосинус: 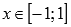 .
.
· Область значений функции y = arccos(x):  .
.
· Функция не является ни четной ни нечетной, то есть, она общего вида.
· Функция арккосинус убывает на всей области определения, то есть, при 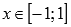 .
.
· Функция вогнутая при  , выпуклая при
, выпуклая при  .
.
· Точка перегиба  .
.
· Асимптот нет.
Функция арктангенс y = arctg(x).
График функции арктангенс имеет вид:

Свойства функции арктангенс y = arctg(x).
· Область определения функции y = arctg(x):  .
.
· Область значений функции арктангенс:  .
.
· Функция арктангенс - нечетная, так как 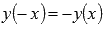 .
.
· Функция возрастает на всей области определения, то есть, при  .
.
· Функция арктангенс вогнутая при  , выпуклая при
, выпуклая при  .
.
· Точка перегиба (0; 0), она же ноль функции.
· Горизонтальными асимптотами являются прямые 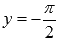 при
при  и
и 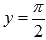 при
при  . На чертеже они показаны зеленым цветом.
. На чертеже они показаны зеленым цветом.
Функция арккотангенс y = arcctg(x).
Изобразим график функции арккотангенс:

Свойства функции арккотангенс y = arcctg(x).
· Областью определения функции арккотангенс является все множество действительных чисел:  .
.
· Область значений функции y = arcctg(x):  .
.
· Функция арккотангенс не является ни четной ни нечетной, то есть, она общего вида.
· Функция убывает на всей области определения, то есть, при  .
.
· Функция вогнутая при  , выпуклая при
, выпуклая при  .
.
· Точка перегиба  .
.
· Горизонтальными асимптотами являются прямые  при
при  (на чертеже показана зеленым цветом) и y = 0 при
(на чертеже показана зеленым цветом) и y = 0 при  .
.
Сложная функция
Если функция y зависит от переменной u, т. е. у = f (u), u  U, а u, в свою очередь, является какой - либо функцией от независимой переменной х, т. е u = g (x), х
U, а u, в свою очередь, является какой - либо функцией от независимой переменной х, т. е u = g (x), х  Х, то переменная у называется функцией от функции (или сложной функцией) от x и записывается в виде Y = f (u), u = g (x), или y = f [ g (x)].
Х, то переменная у называется функцией от функции (или сложной функцией) от x и записывается в виде Y = f (u), u = g (x), или y = f [ g (x)].
Область определения сложной функции - это множество тех значений х  X, для которых функция g (x) определена, кроме того, значения u принадлежат области определения функции y = f (u).
X, для которых функция g (x) определена, кроме того, значения u принадлежат области определения функции y = f (u).
П р и м е р 3. Функция  является сложной. Здесь y = √ u и u = x 2 − 2· x − 3.
является сложной. Здесь y = √ u и u = x 2 − 2· x − 3.
Функция u = x 2 − 2· x − 3 определена на всей числовой прямой, т. е. x  R. В область определения функции y = f (x) входят лишь те значения х, для которых подкоренное выражение неотрицательно x 2 − 2· x − 3 ≥ 0, поэтому х ≤ − 1 и х ≥ 3. Следовательно, D = (− ∞, 1]
R. В область определения функции y = f (x) входят лишь те значения х, для которых подкоренное выражение неотрицательно x 2 − 2· x − 3 ≥ 0, поэтому х ≤ − 1 и х ≥ 3. Следовательно, D = (− ∞, 1]  [3, + ∞). На интервале [− 1, 3] заданная функция не существует.
[3, + ∞). На интервале [− 1, 3] заданная функция не существует.
Из определения следует, что сложная функция у = f [ g (x)] может быть представлена в виде цепочки простых функций: у = f (u), u = g (x). Переменную u принято называть промежуточным аргументом в отличие от независимой переменной х.
Понятие обратной функции
Если функция задана уравнением вида f (x, y) = 0, не разрешенным относительно у, то она при некоторых условиях называется неявной функцией аргумента x.
Пусть задана некоторая функция у = f (х), которая каждому элементу из множества D (f) ставится в соответствие один элемент из множества Е (f). Если обратное соответствие есть тоже функция, то есть, каждому значению у  E(f) соответствует единственное значение х
E(f) соответствует единственное значение х  D (f), то ее называют обратной функцией по отношению к функции f (х).
D (f), то ее называют обратной функцией по отношению к функции f (х).
В этом случае соотношение у = f (х) определяет х как неявную функцию от у. Если это соотношение разрешимо относительно х, то получим явное выражение обратной функции: х = g (у).
Если функция g является обратной по отношению к функции f, то и функция f является обратной по отношению к функции g, т. е. эти две функции - взаимно-обратные.
Одна и та же кривая у = f (х) представляет собой график функции у = f (х) и график обратной функции х = g (у) (если она существует), но в последнем случае значения аргумента рассматриваются на оси Оу, а значения функции - на оси Ох.
Если придерживаться стандартных обозначений и независимую переменную обозначать через х, а функцию − через у, то функция, обратная по отношению к у = f (х), запишется в виде у = g (х). В этом случае график функции у = g (х) симметричен графику функции у = f (х) относительно прямой у = х − биссектрисы I и III координатных углов.
Для взаимно - обратных функций имеют место следующие соотношения
D (f) = E (g), E (f)= D (g),
т. е. область определения данной функции совпадает с множеством значений обратной функции, и наоборот.






