Основные элементарные функции, их свойства и графики

Область определения функции. Необходимые сведения и примеры нахождения.

 

Эта тема очень важна, так как все наши действия с функциями и выражениями возможны лишь на области их определения. С ее нахождения и следует начинать решение практически любых задач.

Определение

Областью определения функции (выражения f(x)) называют множество всех значений x, для которых функция (выражение) имеет смысл.

Область определения функции обозначается как или .

Дальнейшее изложение предполагает знание областей определения основных элементарных функций, знаниеклассификации элементарных функций, а так же умение решать различные виды неравенств и систем неравенств.

При нахождении области определения функции приходится решать различные неравенства (иррациональные, логарифмические, тригонометрические и т.п.) и системы неравенств. Мы не будем подробно останавливаться на их решении, а иногда и вовсе будем оставлять без решения, так как это выходит за рамки данного раздела.

Что указывает на наличие ограничений области определения:

1. присутствие корней четной степени вида 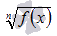, где n - четное, например, (наличие степенной функции с дробным показателем, знаменатель которого есть четное число, например, );Примеры нахождения области определения степенной функции...

 

1. присутствие функции логарифма вида , например, или ; Нахождение области определения логарифмической функции...

 

1. присутствие дробей вида , например, ; Нахождение области определения дроби...

 

1. присутствие функций тангенса вида 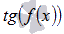и котангенса вида , например, или 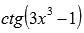; Примеры нахождения области определения тангенса и котангенса...

 

1. присутствие функций арксинуса вида и арккосинуса вида 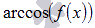, например, 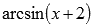или ; Примеры нахождения области определения арксинуса и арккосинуса...

 

1. присутствие показательно степенных функций вида , например, ; Нахождение области определения показательно степенной функции...

 

1. присутствие любых комбинаций всех вышеперечисленных случаев, например,

 

Основные элементарные функции, их свойства и графики.

Знание основных элементарных функций, их свойств и графиков не менее важно, чем знание таблицы умножения. Они как фундамент, на них все основано, из них все строится и к ним все сводится.

В этой статье мы перечислим все основные элементарные функции, приведем их графики и дадим без вывода и доказательств свойства основных элементарных функций по схеме:

· область определения функции;

· поведение функции на границах области определения, вертикальные асимптоты (при необходимости смотрите статью классификация точек разрыва функции);

· проверка на четность и нечетность;

· область значений функции;

· промежутки возрастания и убывания, точки экстремума;

· промежутки выпуклости (выпуклости вверх) и вогнутости (выпуклости вниз), точки перегиба (при необходимости смотрите статью выпуклость функции, направление выпуклости, точки перегиба, условия выпуклости и перегиба);

· наклонные и горизонтальные асимптоты;

· особые точки функций;

· особые свойства некоторых функций (например, наименьший положительный период у тригонометрических функций).

Как эти свойства были получены для каждой из основных элементарных функций можете ознакомиться в разделе полное исследование функции и построение графика.

Если же Вас интересует дифференцирование элементарных функций или интегрирование элементарных функций, то можете перейти к этим разделам теории.

Основными элементарными функциями являются: степенная функция с целым показателем степени, показательная, логарифмическая функция, тригонометрические и обратные тригонометрические функции.

• Степенная функция, ее график и свойства.
• Показательная функция, свойства, график. , где , и
• Логарифмическая функция, ее свойства, графическая иллюстрация. , где , и
• Свойства и графики тригонометрических функций.
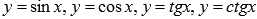
• Обратные тригонометрические функции (аркфункции), их свойства и графики.

Степенная функция.

ЗАМЕЧАНИЯ:

· к основным элементарным степенным функциям относят лишь степенную функцию С ЦЕЛЫМ ПОКАЗАТЕЛЕМ, однако мы рассмотрим все возможные действительные значения показателя степени для общего представления;

· некоторые авторы при рассмотрении степенной функции ограничивают область определения интервалом . Мы же не будем придерживаться этого ограничения. Рекомендем уточнить отношение Вашего преподавателя к этому вопросу во избежании недоразумений. В любом случае все изложенное будет верно (если при области определения рассматривать только этот интервал и отбрасывать все оставшиеся).

Рассмотрим вид и свойства степенной функции в зависимости от значения показателя степени (17 вариантов показателя степени: четный положительный, четный отрицательный, нечетный положительный, нечетный отрицательный, иррациональный, масса вариантов дробно рационального показателя).