Определение: Непрерывная случайная величина Х имеет нормальный закон распределения (закон Гаусса), если ее плотность распределения имеет вид:
,
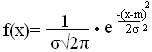где m=M(X), σ2=D(X), σ>0.
Кривую нормального закона распределения называют нормальной или гауссовой кривой (рис.7)
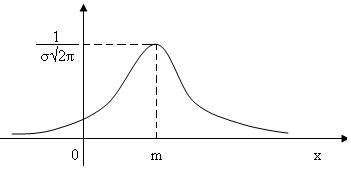Нормальная кривая симметрична относительно прямой х=m, имеет максимум в т. х=а, равный 
.
рис.7
Функция распределения случайной величины Х, распределенной по нормальному закону, выражается через функцию Лапласа Ф (х) по формуле:
,
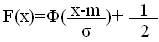где - функция Лапласа.
Замечание: Функция Ф(х) является нечетной (Ф(-х)=-Ф(х)), кроме того, при х>5 можно считать Ф(х) ≈1/2.
График функции распределения F(x) изображен на рис. 8
рис.8
Вероятность того, что случайная величина Х примет значения, принадлежащие интервалу (a;b) вычисляются по формуле:
Вероятность того, что абсолютная величина отклонения меньше положительного числа δ вычисляется по формуле:
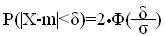
В частности, при m=0 справедливо равенство:
«Правило трех сигм»
Если случайная величина Х имеет нормальный закон распределения с параметрами m и σ, то практически достоверно, что ее значение заключены в интервале (a-3σ; a+3σ), т.к.
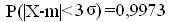
Задача №3. Случайная величина Х распределена нормально с математическим ожиданием 32 и дисперсией 16. Найти: а)плотность распределения вероятностей f(x); б) вероятность того, что в результате испытания Х примет значение из интервала (28;38).
Решение: По условию m=32, σ2=16, следовательно, σ=4, тогда
а)
б) Воспользуемся формулой:
Подставив a=28, b=38, m=32, σ=4, получим
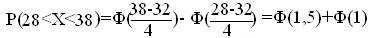
По таблице значений функции Ф(х) находим Ф(1,5)=0,4332, Ф(1)=0,3413.
Итак, искомая вероятность:
P(28<X<38)= 0,4332+0,3413=0,7745.
Задачи для самостоятельной работы
3.1. Случайная величина Х равномерно распределена в интервале (-3;5). Найдите:
а) плотность распределения f(x);
б)функции распределения F(x);
в)числовые характеристики;
г)вероятность Р(4<х<6).
3.2. Случайная величина Х равномерно распределена на отрезке [2;7]. Найдите:
а) плотность распределения f(x);
б)функции распределения F(x);
в)числовые характеристики;
г)вероятность Р(3≤х≤6).
3.3. На шоссе установлен автоматический светофор, в котором 2 минуты для транспорта горит зеленый свет, 3 секунды желтый и 30 секунд красный и т.д. Машина проезжает по шоссе в случайный момент времени. Найти вероятность того, что машина проедет мимо светофора, не останавливаясь.
3.4. Поезда метрополитена идут регулярно с интервалом 2 минуты. Пассажир выходит на платформу в случайный момент времени. Какова вероятность того, что ждать поезд пассажиру придется больше 50 секунд. Найти математическое ожидание случайной величины Х- время ожидания поезда.
3.5. Найти дисперсию и среднее квадратическое отклонение показательного распределения, заданного функцией распределения:
F(x)= 0 при х<0,
1-е-8х при х≥0.
3.6. Непрерывная случайная величина Х задана плотностью распределения вероятностей:
f(x)= 0 при х<0,
0,7•е-0,7х при х≥0.
а) Назовите закон распределения рассматриваемой случайной величины.
б) Найдите функцию распределения F(X) и числовые характеристики случайной величины Х.
3.7. Случайная величина Х распределена по показательному закону, заданному плотностью распределения вероятностей:
f(x)= 0 при х<0,
0,4 •е-0,4 х при х≥0.
Найти вероятность того, что в результате испытания Х примет значение из интервала (2,5;5).
3.8. Непрерывная случайная величина Х распределена по показательному закону, заданному функцией распределения:
 |
F(x)= 0 при х<0,
1-е-0,6х при х≥0
Найти вероятность того, что в результате испытания Х примет значение из отрезка [2;5].
3.9. Математическое ожидание и среднее квадратическое отклонение нормально распределенной случайной величины соответственно равны 8 и 2. Найдите:
а) плотность распределения f(x);
б) вероятность того, что в результате испытания Х примет значение из интервала (10;14).
3.10. Случайная величина Х распределена нормально с математическим ожиданием 3,5 и дисперсией 0,04. Найдите:
а) плотность распределения f(x);
б) вероятность того, что в результате испытания Х примет значение из отрезка [3,1;3,7].
3.11. Случайная величина Х распределена нормально с M(X)=0 и D(X)=1. Какое из событий: |Х|≤0,6 или |Х|≥0,6 имеет большую вероятность?
3.12. Случайная величина Х распределена нормально с M(X)=0 и D(X)=1.Из какого интервала (-0,5;-0,1) или (1;2) при одном испытании она примет значение с большей вероятностью?
3.13. Текущая цена за одну акцию может быть смоделирована с помощью нормального закона распределения с M(X)=10ден.ед. и σ (Х)=0,3 ден.ед. Найти:
а) вероятность того, что текущая цена акции будет от 9,8 ден.ед. до 10,4 ден.ед.;
б)с помощью «правила трех сигм» найти границы, в которых будет находится текущая цена акции.
3.14. Производится взвешивание вещества без систематических ошибок. Случайные ошибки взвешивания подчинены нормальному закону со средним квадратическим отношением σ=5г. Найти вероятность того, что в четырех независимых опытах ошибка при трех взвешиваниях не произойдет по абсолютной величине 3г.
3.15. Случайная величина Х распределена нормально с M(X)=12,6. Вероятность попадания случайной величины в интервал (11,4;13,8) равна 0,6826. Найдите среднее квадратическое отклонение σ.
3.16. Случайная величина Х распределена нормально с M(X)=12 и D(X)=36.Найти интервал, в который с вероятностью 0,9973 попадет в результате испытания случайная величина Х.
3.17. Деталь, изготовленная автоматом, считается бракованной, если отклонение Х ее контролируемого параметра от номинала превышает по модулю 2 единицы измерения. Предполагается, что случайная величина Х распределена нормально с M(X)=0 и σ(Х)=0,7. Сколько процентов бракованных деталей выдает автомат?
3.18. Параметр Х детали распределен нормально с математическим ожиданием 2, равным номиналу, и средним квадратическим отклонением 0,014. Найти вероятность того, что отклонение Х от номинала по модулю не превысит 1% номинала.
Ответы
3.1.
0 при х≤-3,
а) f(х)= 1/8 при -3<х<5,
0 при х≥5.
б) 0 при х≤-3,
F(х)= 
при -3<х≤5,
1 при х>5.
в) M(X)=1, D(X)=16/3 σ (Х)= 4/√3
г)1/8.
3.2.
0 при х<2,
а) f(х)= 1/5 при 2≤х≤7,
0 при х>7.
б) 0 при х≤2,
F(х)=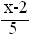 
при 2<х≤7,
1 при х>7.
 |
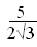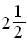
в) M(X)=4,5,D(X) =, σ (Х)=
г)3/5.
3.3. 40/51.
3.4. 7/12, M(X)=1.
3.5. D(X) = 1/64, σ (Х)=1/8
3.6. F(x)= 0, при х<0,
1-е-0,7х при х≥0.
 |  |  | |||
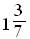M(X)=,D(X) =, σ (Х)=.
3.7. Р(2,5<Х<5)=е -1-е-2≈0,2325
3.8. Р(2≤Х≤5)=0,252.
 |
3.9. а)
б) Р(10<Х<14)≈0,1574.
 |
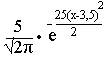3.10. а)f(x)=,
б) Р(3,1≤Х≤3,7) ≈0,8185.
3.11. |x|≥0,6.
3.12. (-0,5;-0,1).
3.13. а) Р(9,8≤Х≤10,4) ≈0,6562.
б)(9,1;10,9)
3.14. 0,111.
3.15. σ=1,2.
3.16. (-6;30).
3.17. 0,4%.
3.18. 0,8472.
