Прямая и обратная геодезические задачи на плоскости

 

Именно – на плоскости. Потому что есть прямая и обратная геодезические задачи на земном эллипсоиде. Вам придется их решать в курсе «Высшей геодезии». Тогда Вы и познаете большую разницу. Кривизна Земли, её форма дадут это почувствовать.

Название «прямая» и «обратная» геодезические задачи несколько условные, но уже теперь традиционно принятые в геодезии и маркшейдерии раз и навсегда. Просто одну из задач назвали прямой, при решении которой находят координаты точек местности, а другую – обратной, при решении которой …

Давайте не будем забегать вперед.

Прямая геодезическая задача.

Пусть нам известны координаты точки 1 (Х₁, Y₁), горизонтальное проложение линии 1-2 d₁₂ и её дирекционный угол α₁₂ (рис. 7.3). Требуется найти координаты точки 2. Таковы условия прямой геодезической задачи.

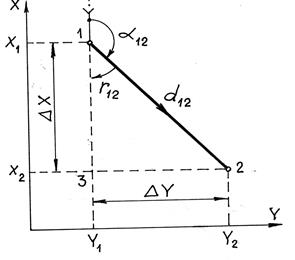
Рис. 7.3. Прямая и обратная геодезические задачи на плоскости.

Прямая геодезическая задача используется для определения координат точек местности, в частности, при определении координат точек теодолитных ходов. Поскольку указанная задача решается на плоскости (в проекции Гаусса-Крюгера), то треугольник 123 является прямоугольным. Линия 1-2 ориентирована (на рисунке) в круговой (α) и четвертной (r) системах. Параметры Δ Х и Δ Y называют приращениями координат. Исходя из геометрии и принятой системы координат можно записать, что

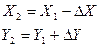. (7.1)

Очевидно, что приращения координат должны иметь знак «плюс» или «минус», поскольку координаты точки 2 могут быть больше или меньше координат точки 1. Не обращая внимания на знаки приращений координат, запишем из прямоугольного треугольника

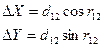. (7.2)

Принимая во внимание схему рис. 6.3, запишем, что

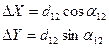, (7.3)

т.е. знаки приращений координат определяются знаками функций sin и cos соответствующих дирекционных углов. Тогда для общего случая формулы (7.1) примут вид

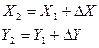. (7.4)

Пример 7.1. Прямая геодезическая задача.

Исходные данные: Х₁ = 4256,324 м; Y₁ = 7830,042 м; α₁₂ = 248^о39'42"; d₁₂ = 211,656 м.

Найти координаты точки 2.

Решение.

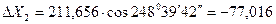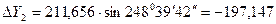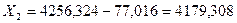м;

м;

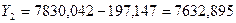м;

м.

 

Обратная геодезическая задача.

Формулировка обратной геодезической задачи: по известным координатам двух точек найти горизонтальное проложение линии, соединяющей эти точки и её дирекционный угол.

Применительно к рис. 7.3: по известным координатам точек 1 и 2 найти горизонтальное проложение d₁₂ и дирекционный угол α₁₂.

Обратная геодезическая задача используется в большом числе случаев при определении дирекционных углов исходных направлений, а также при решении различных геометрических задач на местности, связанных с построением на местности проектных точек инженерных сооружений (Геодезические разбивочные работы).

Установим взаимосвязь между знаками приращений координат и значениями дирекционных углов (табл. 7.2).

Для решения обратной геодезической задачи вычисляют приращения координат

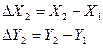, (7.5)

если задана задача определения дирекционного угла направления 1-2. Если же необходимо определить дирекционный угол направления 2-1, то приращения координат определяют по формулам

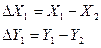. (7.6)

Далее вычисляют значение румба определяемого направления без учёта знаков приращений координат

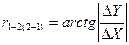(7.7)

и по знакам приращений координат, пользуясь табл. 7.2, выбирают соответствующую формулу для вычисления дирекционного угла.

Таблица 7.2

Знаки приращений координат в зависимости от величины дирекционного угла

Δ Х	+	-	-	+
Δ Y	+	+	-	-
Четверть	I(СВ)	II(ЮВ)	III(ЮЗ)	IV(СЗ)
Изменения дирекционного угла	0о – 90о	90о – 180о	180о – 270о	270о – 360о(0о)
Зависимость α = f (r)	α = r	α = 180o - r	α = 180o + r	α = 360o - r

 

Дирекционный угол линии можно определить, таким образом, для любого её направления, а дирекционный угол обратного направления, при необходимости, определяют по формуле обратного ориентирующего угла: .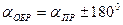

Горизонтальное проложение из прямоугольного треугольника 123 находят по формулам:

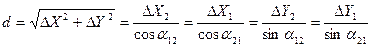. (7.8)

Значения горизонтальных проложений, вычисленных по приведённым формулам, должны практически совпадать в пределах погрешностей округлений.

 

Пример 7.2. Обратная геодезическая задача.

Исходные данные: Х₁ =7273,856 м; Y₁ = 5241,656 м; Х₂ = 9833,813 м; Y₂ = 2165,041 м

Найти дирекционный угол направления 1-2 и горизонтальное проложение линии 1-2.

Решение.

Δ Х₂ = 9833,813 – 7273,856 = + 2559,957 м.

Δ Y₂ = 2165,041 – 5241,656 = - 3076,615 м.

(Четвертая четверть – СЗ) – см. табл. 7.2.

.

.

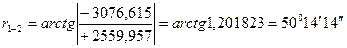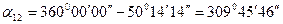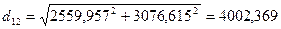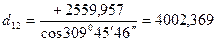м;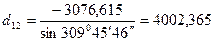

м; м.

Незначительные расхождения в значениях горизонтального проложения обусловлены погрешностями вычислений при округлении приращений координат и дирекционного угла.

Обратный дирекционный угол .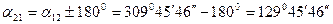

Этот угол может быть получен и прямым расчётом через соответствующие приращения координат:

Δ Х₁ = 7273,856– 9833,813 = - 2559,957 м.

Δ Y₁ = 5241,656–2165,041= + 3076,615 м.

(Вторая четверть – ЮВ) – см. табл. 7.2.

.

.
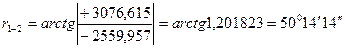
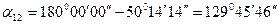