Определение размера страховых запасов

На рис. 89 представлен идеальный вариант движения запаса: расход осуществляется равномерно, новая партия поступает на склад точно в момент полного расхода предыдущей. На практике фактический расход запаса неравномерен и может превышать плановый. Поступление заказанных товаров по вине поставщиков или перевозчиков может запаздывать. В связи с этим предприятия создают страховые запасы. Цель создания страховых запасов — обеспечить непрерывность торгового или производственного процесса в следующих случаях:

• задержка поставщиком срока отгрузки заказа;

• задержка товара в пути при доставке от поставщика;

• непредвиденное возрастание объема сбыта.

Перечисленные ситуации не планируют, но, поскольку они возможны, их ожидают и к ним готовятся, создавая страховые запасы.

Страховой запас позволяет стабильно функционировать в условиях плохо отрегулированных хозяйственных отношений и неизбежных ошибок при прогнозировании и последующем планировании спроса.

Страховой запас не является неприкосновенным. Расход этой компоненты общего запаса также неизбежен, как и неизбежны погрешности планирования и организации поставок. Однако при запланированном ходе поставок и стабильном, соответствующем плану сбыте, величина страхового запаса, в отличие от текущего, не меняется.

Страховой запас, так же как и текущий, имеет двойственный характер, т. е. играет как положительную, так и отрицательную роль. Значительный страховой запас способен покрыть все случайные отклонения. Предприятие сможет избежать потерь оборота и имиджа, вызванных отсутствием в нужный момент запасов на складе, т. е. потерь от дефицита. Однако это может привести к неоправданно большим затратам на содержание страхового запаса на складе компании.

Определяющим экономическим фактором при расчете величины страхового запаса является достижение минимальных суммарных потерь и затрат, вызванных дефицитом и содержанием запаса.

На величину потребности в страховых запасах оказывает влияние следующие основные факторы:

• вероятность того, что поставщик нарушит свои обязательства по отгрузке товаров (по сроку или по количеству, или по тому и другому вместе);

• вероятность незапланированного роста потребности в товарах (роста сбыта);

• вероятность того, что перевозчик нарушит свои обязательства по срокам доставки товаров.

Возможно также влияние других факторов.

Кроме того, на размер страховых запасов влияет характер распределения таких случайных величин, как сроки поставок, объемы сбыта и др.

Существенное влияние на потребность в страховых запасах оказывает допускаемая в конкретной ситуации вероятность возникновения дефицита. Например, при снижении допускаемой вероятности дефицита с сорока до одного процента в условиях нормально распределенного спроса потребность в страховых запасах увеличивается более чем в девять раз (в 9,32 раза).

Количественная оценка каждого из перечисленных выше факторов, а также учет их совместного влияния на размер страхового запаса в единой аналитической модели является сложной научной задачей, требующей к тому же обширной информационной поддержки.

Рассмотрим более простую хорошо изученную ситуацию определения оптимального страхового запаса, когда имеется только одна случайная величина, т. е. действует лишь один случайный фактор.

Первый вариант однофакторной ситуации:

• сроки поставок на склад подвержены случайным колебаниям;

• сбыт со склада за любой период точно соответствует плану.

Такая ситуация может иметь место, например, для центрального склада системы: "центральный склад компании — склады филиалов".

Сроки поставок на центральный склад от поставщиков могут непредсказуемо отклоняться от плановых. Объемы и сроки отгрузок с центрального склада компании на склады филиалов (объемы сбыта) точно определены.

Второй вариант однофакторной ситуации:

• сроки поставок на склад точно соответствуют планам,

• сбыт в периоды между поставками подвержен случайным колебаниям.

В системе "центральный склад компании — склады филиалов" такая ситуация может иметь место на складах филиалов: внутрисистемные поставки с центрального склада детерминированы, а сбыт носит неопределенный, стохастический характер.

Расчет размера страхового запаса по однофакторной ситуации, выполняется на основе статистических данных о фактических значениях случайного фактора, например:

• данные о сроках выполнения заказов поставщиком за предшествующие 12 месяцев (вариант 1),

• данные о величине сбыта в периоды между поставками за последние 12 месяцев (вариант 2).

Рассмотрим порядок расчета оптимального размера страхового запаса в случае, когда срок и объемы поставок на склад четко соблюдаются, а величина сбыта в периоды между поставками имеет случайный характер (вариант 2).

Вначале, пользуясь данными статистического ряда, необходимо определить закон распределения случайной величины. В том случае, если распределение имеет нормальный характер[77], размер страхового запаса (R) рассчитывают по формуле

R = t · σ.

где σ— среднее квадратическое отклонение величины сбыта за периоды поставки;

t — параметр нормального закона распределения (параметр функции Лапласа).

Параметр t определяется на основе решения о допустимой вероятности наличия дефицита (а).

Последовательность определения параметра t:

1) определить оптимальную вероятность возникновения дефицита, величину а;

2) определить значение функции Лапласа F(t) для найденной вероятности возникновения дефицита;

3) определить значение параметра t для найденного значения функции Лапласа F(t).

Остановимся подробнее на характеристике каждого из действий.

1. Определение оптимальной вероятности возникновения дефицита.

Из теории управления запасами известно, что уровень страхового запаса R при наличии только одной случайной величины — потребности между двумя смежными поставками — должен быть таким, чтобы вероятность возникновения дефицита (а) определялась выражением

а = ,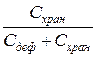

где С_храм — затраты на хранение единицы товара на складе в единицу времени;

С_деф — потери из-за дефицита (отсутствия) товара на складе в единицу времени.

Например, затраты на хранение единицы товара составляют С_хран = 180 руб/год, а потери от дефицита С_деф= 4320 руб./год. Тогда вероятность возникновения дефицита должна составлять[78]

а = 0,04.

Вероятность возникновения дефицита может быть определена также из заданного руководством Компании или службой маркетинга уровня сервиса η, выраженного в долях от единицы. Тогда:

а = 1– η.

2. Определение значения функции Лапласа F(t) для найденной вероятности возникновения дефицита.

График плотности нормального распределения приведен на рис. 93. Напомним, что общая площадь под кривой равна единице, т. е. суммарной вероятности всех возможных значений сбыта. Наибольшую вероятность имеет среднее значение величины сбыта за период поставки. Чем больше отклонение значения сбыта от центра рассеивания, тем меньше вероятность этого события. Площадь правой заштрихованной области на графике равна допустимой вероятности дефицита (а). Заштрихуем равный участок слева. Площадь оставшейся незаштрихованной части графика (значение функции Лапласа) находим по формуле

F(t) = l – 2 a.

В нашем примере F(t)= 1 – 2 × 0,04=0,92.

 

 

Рис. 93. Плотность нормального распределения

 

3. Определение значения параметра t для найденного значения функции Лапласа F (t).

Пользуясь полученным значением функции F(t), по таблицам нормального распределения находим значение аргумента (параметр t).

Значения функции Лапласа, а также соответствующие значения уровня сервиса для некоторых значений t приведены в табл. 23.

В нашем примере t =1,75.

Таблица 23

Значения функции Лапласа и соответствующие значение уровня сервиса при разных значениях t

t Параметр функции Лапласа	Ф(t) Нормированная функция Лапласа (с округлением до 3-го знака)	а Вероятность наличия дефицита	η Уровень сервиса в долях от единицы	η Уровень сервиса в процентах
0,00	0,000	0,50	0,50
0,13	0,103	0,45	0,55
0,25	0,197	0,40	0,60
0,39	0,303	0,35	0,65
0,52	0,397	0,30	0,70
0,53	0,404	0,30	0,70
0,67	0,497	0,25	0,75
0,84	0,599	0,20	0,80
1,04	0,702	0,15	0,85
1,28	0,799	0,10	0,90
1,34	0,820	0,09	0,91
1,41	0,841	0,08	0,92
1,48	0,861	0,07	0,93
1,56	0,881	0,06	0,94
1,65	0,901	0,05	0,95
1,75	0,920	0,04	0,96
1,88	0,940	0,03	0,97
2,05	0,960	0,02	0,98
2,33	0,980	0,01	0,99
2,37	0,982	0,009	0,991	99,1
2,41	0,984	0,008	0,992	99,2
2,45	0,986	0,007	0,993	99,3
2,51	0,988	0,006	0,994	99,4
2,57	0,990	0,005	0,995	99,5

 

Среднее квадратическое отклонение (σ), входящее в формулу страхового запаса, рассчитывается следующим образом:

σ =

где х_i — случайная величина (в нашем примере величина сбыта во время i -й поставки);

— средняя арифметическая случайной величины;

п — количество значений случайной величины (объем статистики).

Продолжим наш пример и рассчитаем размер страхового запаса. Воспользуемся для этого статистикой значений сбыта в периоды между поставками за последние 12 месяцев (табл. 24).

Таблица 24