И метода определения момента инерции

Маятник Обербека представляет собой крестовину, состоящую из втулки 1, четырех спиц 2, укрепленных на одном из концов втулки. На спицах размещены грузы 3. Последние могут перемещаться вдоль спиц и закрепляться на них с помощью винтов. Другой конец втулки выполнен в виде шкива 4, на который наматывается нить-шнур. К свободному концу шнура привязан груз 5. Под влиянием этого груза маятник приходит в ускоренное вращательное движение вокруг непо­д­вижной оси. Трение между втулкой маятника и осью практически сведено к нулю установленными на ось подшипниками. Для установки груза 5 на определенной высоте предусмотрен указатель 6. Исходным уравнением для определения момента инер­ции I маятника является основной закон динамики вращательного движения, из которого следует, что

, (2.1)

где M ‒ вращающий момент, в данном случае момент силы Т ₁ натяжения шнура, приложенной в точке К (рис.2.1); 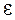‒ угловое ускорение маятника. Мо­мент силы берется отно­сительно оси вращения, а потому

М = T ₁ R, (2.2)

где R - радиус шкива.

Сила T ₁ = Т ₂ = Т, которая может быть найдена из второго закона Ньютона. записанного для груза 5:

ma = mg – T ₂,

где m - масса груза 5; а - ускорение, с которым он опускается, откуда

Т = m (g - а). (2.3)

Таким образом, подставляя (2.3) в (2.2), получим

М = m(g - a) R. (2.4)

Угловое ускорение 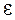связано с тангенциальным ускорением точек на ободе колеса следующим соотношением:

.

В свою очередь, 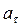совпадает с ускорением а, с которым опускается груз 5. Следовательно,

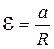. (2.5)

Ускорение а можно вычислить, если измерить время t опускания груза 5 на определенную высоту h. Действительно

,

откуда

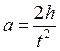. (2.6)

Подставляя (2.6) в (2.5) и (2.4), а затем в (2.1), получим

 

, (2.7)

где d = 2 R ‒ диаметр шкива.

Заметим, что второе слагаемое в выражении (2.7) оказывается на практике значительно меньше первого, а потому момент инерции маятника можно вычислить как

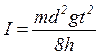. (2.8)

Порядок выполнения работы

 

1. Внесите в таблицу данные о массе груза 5 и ускорении свободного падения для широты г. Пермь (написаны на приборе).

2. Установите грузы 4 на концы спиц, причем так, чтобы маятник находился в безразличном равновесии.

3. Наматывая нить на шкив, установите груз 5 так, чтобы основание груза совпало с указателем 6 (см. рис.2.1), (следите за тем, чтобы витки нити на шкив наматывались в один слой, а нить намоталась бы с внешней стороны маятника). В этом положении маятник придерживайте рукой за одну из спиц.

4. Измерьте время t ₁опускания груза 5 с установленной высоты до пола. Для чего отпустите маятник без толчка, включив одновременно секундомер. Опыт повторите не менее 7 раз. Результаты занесите в таблицу.

5. Передвиньте грузы 3 примерно на середину спиц и установите их так, чтобы маятник находился в безразличном равновесии.

По п. 4 измерьте время t ₂ движения груза в этом случае. Результаты запишите в таблицу.

6. Измерьте диаметр шкива d и высоту падения груза h, оцените ошибкиD d иD h в измерении этих величин. Данные занесите в таблицу.

 

Номер опыта	t 1	t 2	t 1 i - < t 1 >	(t 1 i - <t 1 >)2	Другие данные
. . .					g = … ± … d =… ± … h =… ± … a = …, D t пр =
	S t 1 =	S t 2 =	S(t 1 i - < t 1 >)2 =
	<t 1 > =	<t 2 > =

7. Вычислите < > и < 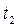> и по формуле

< I > = ,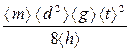

вычислите среднее значение моментов инерци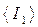и и 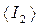(для того и другого расположения грузов 3).

8. Определите абсолютную и относительную погрешности в определении момента инерции (только для или только для 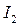, так как погрешности будут приблизительно одинаковыми).

Для чего:

а) задайтесь надежностью a (0,95), выберите коэффициент Стьюдента 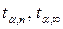, оцените D t _пр для секундомера;

б) вычислите абсолютную погрешность в измерении времени:

;

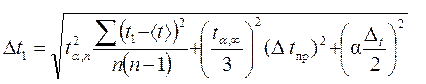в) вычислите относительную погрешность в определении I (например, I ):

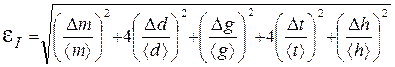
г) вычислите абсолютную погрешность:

;

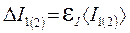д) результаты запишите в виде

, .

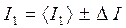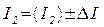при a =..., %,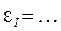

9. Сравнивая I ₁и I ₂, сделайте вывод (касающийся связи величины момента инерции и расположения грузов 3).

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Что называется моментом инерции материальной точки относительно оси, моментом инерции твердого тела относительно оси?

В каких единицах измеряется момент инерции?

2. В чем состоит теорема Штейнера? Приведите пример ее использования.

3. Что называется моментом силы относительно оси? В каких единицах он измеряется?

4. Что такое плечо силы?

5. Что называется моментом импульса материальной точки относительно оси вращения, моментом импульса твердого тела относительно оси вращения? В каких единицах измеряется момент импульса?

6. Как связаны между собой момент импульса и момент инерции тела, вычисленные относительно оси вращения?

7. Маятник Обербека: устройство и теория метода определения его инерции.

8. Порядок выполнения работы. Выводы.

 

 

ЛАБОРАТОРНАЯ РАБОТА № 3

ФИЗИЧЕСКИЙ МАЯТНИК

Цель: познакомиться с методом определения моментов инерции тел.

Приборы и принадлежности: исследуемое тело (пластина), кронштейн для подвешивания тела, секундомер, линейка, математический маятник.

Сведения из теории

Подробно теоретические сведения для данной лабораторной работы изложены в разделе 1.3.2. Маятники (стр. 52-56 данного учебного пособия).

 

Описание установки