Принято различать три типа ошибок погрешностей прямых измерений: промахи, систематические погрешности и случайные погрешности.
1. Промахи -грубые ошибки, существенно превышающие ожидаемую при данных условиях погрешность. Они вызываются невнимательностью экспериментатора, использованием неисправных приборов и т.д. Как правило, промахи быстро выявляются и наблюдения, содержащие их, следует отбрасывать, как не заслуживающие доверия.
2. Случайные погрешности - погрешности, вызванные большим числом случайных неконтролируемых помех (сотрясением фундамента здания, изменением напряжения электрической сети, реакцией наблюдателя). В итоге при повторных наблюдениях получаются несколько отличающиеся друг от друга результаты. Исключить случайные погрешности нельзя, можно лишь оценить их величину. Как это сделать, нам подсказывает так называемая теория погрешностей. В основе этой теории лежат два предположения, подтверждаемых опытом:
а) при большом числе измерений случайные погрешности одинаковой величины, но разного знака встречаются одинаково часто;
б) большие (по абсолютной величине) погрешности встречаются реже, чем малые.
Из этих предположений следует, что при многократных измерениях величины х наиболее близким к ее истинному значению 
х 0 является среднее арифметическое значение:
, (1.2)
где n - число измерений.
Упомянутая выше теория погрешностей дает возможность найти величину случайной погрешности D хсл, т.е. расхождение между х 0 и < x >. При этом исходят из следующих соображений.
Пусть a характеризует вероятность того, что истинное значение х 0 измеряемой величины отличается от < x > на величину, не большую D х сл, т.е. вероятность того, что истинное значение попадет в интервал от < x > - D x сл до < x >+D x сл (рис. 1.1). Например, если a = 0,95, то это означает, что примногократных повторениях опыта ошибки отдельных измерений в 95 случаях из 100 не превысят значения D х сл. Вероятность a называется доверительной вероятностью или надежностью, а интервал значений (< x >± D x сл) - доверительным интервалом. Как видно, D x сл - это полуширина доверительного интервала. Ее-то и принимают за абсолютную случайную погрешность.
Задача, очевидно, состоит в том, чтобы отыскать Dxсл при наперед заданном значении a. Решению этого вопроса помогает существующая между Dxсл и a математическая связь. Качественно эта связь ясна: чем с большей надежностью мы хотим указать результат данных измерений, тем больше должен быть доверительный интервал.
В теории погрешностей в качестве единицы ширины доверительного интервала выбрана так называемая средняя квадратичная погрешностьрезультата измерений
. (1.3)
Здесь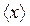 
‒ среднее для измеренных n значений 
(i = 1, 2, 3,…, n); 
‒ отклонение i -го наблюдения от среднего значения, n ‒ число измерений.
В случае небольшого числа измерений (именно так обстоит дело в учебных лабораториях) было предложено вычислять полуширину доверительного интервала по формуле:
, (1. 4)
где ta,n ‒ коэффициент Стьюдента (зависит от a и n). Зависимость ta,n от n понятна: чем больше n, тем меньше 
отличается от истинного значения, и тем меньше будет доверительный интервал, точнее результат измерения, а значит меньше ta,n.
3. Систематическими называются погрешности, которые сохраняют свою величину и знак во всех однородных (одинаковых) измерениях. Систематические ошибки вызываются разными причинами, односторонне влияющими на результат измерений:
‒ ограниченной точностью приборов (измерительных инструментов) - приборные (инструментальные погрешности;
‒ неправильной настройкой (неравные плечи весов, стрелка не установлена на ноль и т.д.);
‒ в расчетных формулах не учтено влияние некоторых второстепенных факторов (например, при взвешивании не учитывается сила Архимеда, при измерении электросопротивления не учитывается сопротивление проводящих проводов);
‒ округлениями, которые производятся при измерениях и вычислениях.
В большем числе случаев систематические погрешности могут быть изучены и скомпенсированы путем внесения поправок в результаты измерений. Если же сделать этого нельзя (или сложно) необходимо правильно учесть вклад систематической ошибки в общую ошибку измерений.
При выполнении лабораторных работ приходится оценивать, как правило, следующие систематические ошибки:
а) Приборную (инструментальную) погрешность. Погрешность показания прибора (например, связанная с неправильностью разбивки шкалы амперметра, линейки...) является вполне определенной. При обработке результатов измерений этот вид погрешностей задается в виде так называемой предельной погрешности прибора ( коротко - приборной погрешности), указывающей, какова максимально возможная погрешность при использовании данного прибора. При этом для одних приборов указывается предельная абсолютная погрешность D х пр, 
для других (электроизмерительных, части оптических) предельная относительная погрешность (класс точности прибора k).
Классом точности прибора называется отношение предельной абсолютной погрешности к максимальному значению измеряемой прибором величины
. (1.5)
Классов точности семь: 0,02; 0,05; 0,1; 0,5; 1; 2,5; 4. Это число указано на шкале прибора. Зная класс точности и пределы измерения прибора, можно рассчитать его предельную погрешность
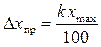. (1.6)
Приборная погрешность других приборов равна точности измерительного прибора, под которой понимают ту наименьшую величину, которую можно надежно определить с помощью данного прибора. Точность прибора зависит от цены наименьшего деления его шкалы и указывается на самом приборе или в его паспорте. Если этих данных нет, то пользуются следующими правилами. Если прибор снабжен нониусом (например, штангенциркуль), то его точность (и приборная погрешность) равна цене наименьшего деленияD х пр=D. При этомD = l / m, где l - цена наименьшего деления основной шкалы прибора, m ‒ число делений нониуса; при отсутствии нониуса (линейка, термометр,...) приборная погрешностьравна половине наименьшего деления шкалы прибора: 
.
Приборная погрешность D х пр представляет собой наибольшую погрешность, даваемую прибором. Действительная же погрешность прибора 
(стандартное отклонение) носит случайный характер и меньше D х пр. Строгих формул для перевода D х пр в нет, чаще всего пользуются выражением
(1.7)
где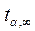 
- коэффициент Стьюдента при n = ¥.
Примечание: для электроизмерительных приборов D х пр не зависит от значения измеряемой величины х изм. Относительная же погрешность измерения, т.е. D х пр / х изм, зависит от х изм: чем больше х изм, тем меньше относительная погрешность. Поэтому при измерениях рекомендуется выбирать такие пределы измерения, чтобы отсчеты на них производились бы по второй половине шкалы прибора.
б) Погрешность округления при измерении. При измерениях показания приборов часто лежат между делениями шкалы. Отсчет “на глаз” долей деления затруднительны. Поэтому показания приборов, как правило, округляются - возникает погрешность округления при измерениях.
Интервал округления может быть различным. Чаще всего это либо цена наименьшего деления шкалы - D, либо половина цены деления. Очевидно, максимальная погрешность округления равна половине интервала округления, т.е. величине D/2. Действительная же погрешность меньше, и при доверительной вероятностиa за погрешность округления принимают величину
. (1.8)
в) Погрешность округления при вычислениях. Этот вид погрешности приходится учитывать только при косвенных измерениях. По этой причине сведения по данной погрешности в следующем разделе.
4. Полная погрешность. Как уже отмечалось, в реальных условиях присутствуют как случайные, так и систематические погрешности. В теории вероятности показывается, что погрешность, обусловленная несколькими независимыми причинами, определяется квадратичным суммированием, т. е. полная абсолютная погрешность прямого измерения
(1.9)
Относительная погрешность
(1.10)
При этом доверительная вероятность a выбирается одинаковой для всех видов погрешностей.
Некоторые из слагаемых под знаком корня могут быть настолько малыми по сравнению с другими, что ими можно пренебречь (малыми считаются ошибки, которые не превышают 30 % от максимальной).
В заключение отметим, что количество необходимых измерений определяется соотношением приборной и случайной погрешностей. Если при повторных измерениях получается одно и то же значение, то это означает, что случайная погрешность в данном методе измерений значительно меньше приборной и большее число измерений не изменит общей ошибки.
При значительной случайной погрешности (при повторных измерениях получаются отличные друг от друга значения) число измерений лучше выбрать таким, чтобы случайная погрешность среднего арифметического была меньше приборной, или, по крайней мере, одного с ней порядка.
Погрешность однократного измерения можно принять равной погрешности прибора.
