Так как исследуемая система нелинейная, то для анализа возникновений автоколебаний ее необходимо линеаризовать. Воспользуемся методом гармонической линеаризации: разложить выходной сигнал НЭ в ряд Фурье, а затем оставить только первую гармонику.
НЭ при осуществлении гармонической линеаризации заменяется эквивалентным комплексным коэффициентом передачи:
Автоколебательный режим в гармонически линеаризованной системе может существовать, если она находится на колебательной границе устойчивости. При этом обычно используют необходимые условия нахождения на границе устойчивости. Например, на основе критерия устойчивости Найквиста можно записать
(33)
Из этого условия можно найти параметры AП и wП, соответствующие режиму автоколебаний в системе.
Для решения этого уравнения воспользуемся методом построения годографов левой и правой части. Для этого преобразуем (33) к виду:
где правая часть уравнения- обратный комплексный коэффициент передачи.
Так как НЭ представлен нелинейностью типа «ограничение», то 
примет вид:
где а - ограничение на зону линейности. Согласно ТЗ, a =4 В. Будем считать, что коэффициент наклона нелинейной характеристики УМ равен 1, а коэффициент передачи УМ будем рассматривать отдельно, как часть линейной системы. Отметим, что формула (33) справедлива только при А ≥ а.
Сформулируем условие появления автоколебаний: автоколебания возникнут, если годограф линейной части системы пересечет годограф обратного комплексного коэффициента передачи. Точка пересечения даст значения амплитуды и частоты гармонического сигнала, вызывающего автоколебания.
Построим годографы левой и правой частей уравнения (34):
Рисунок 21 - Годографы линейной и нелинейной частей системы(увеличенный масштаб)
Как видно из рисунка, у годографов нет точек пересечения, а значит, равенство (33) не выполняется не при каких значениях частоты и амплитуды. Т.е. при наличии насыщения в УМ, режим автоколебаний невозможен.
Заключение
В результате проделанной работы для заданной в ТЗ системы был синтезирован КУ – регулятор, позволяющий достичь требуемого качества. Синтез регулятора осуществлялся на основе: П-регулятора; ПД-регулятора; метод синтеза желаемой ЛАЧХ. По результатом сравнения полученных КУ был выбран лучший регулятор, имеющий более простую структуру и высокие показатели качества.
Проектируемая система испытывалась при отработке типовых входных воздействий, перечисленных в ТЗ.
При учете нелинейности, была исследована реакция нелинейной системы с насыщением УМ на входной ступенчатый сигнал. Были отмечены отличия нелинейной системы от линейной при воспроизведении этого сигнала. Для эффективного и надежного использования спроектированной САР была указан желаемый диапазон входных сигналов для работы системы в зоне линейного усиления.
Библиографический список
1. Бесекерский В.А., Попов Е.П. Теория систем автоматического регулирования. М.:Наука, 1975.
2.Макаров И.М., Менский Б.М. Линейные автоматические системы. —М.: Машиностроение, 1982.
Приложение А
Проверка исходной системы требованиям ТЗ.
Получение переходной характеристики
Рисунок 22 - Получение
t≈0.44c.
Приложение B.
Анализ устойчивости системы по критерию Найквиста.
Рисунок 23 - Построение ЛАЧХ и ЛФЧХ
Приложение C
Проверка системы с пропорциональным регулятором требованиям ТЗ.
Получение переходной характеристики
Рисунок 23 – Получение переходной характеристики при введении пропорционального регулятора
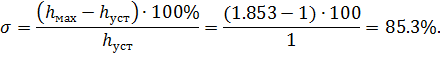
t>2c.
Приложение D
Определение коэффициента усиления в ПД-регуляторе 
ХУ ЗС и его коэффициенты:
Определение диапазона К по критерию Гурвица.
1) Необходимое условие:
2) Достаточное условие:
Исходя из полученных результатов, определим диапазон значений К:
Приложение E
Проверка системы с ПД-регулятором по прямым показателям качества.
Рассмотрим 2 случая: первый – когда выбранное значение коэффициента К обеспечивает соответствие системы ТЗ, второй – когда не соответствует.
1) 
Получение переходной характеристики и построение графика системы, соответствующей ТЗ.
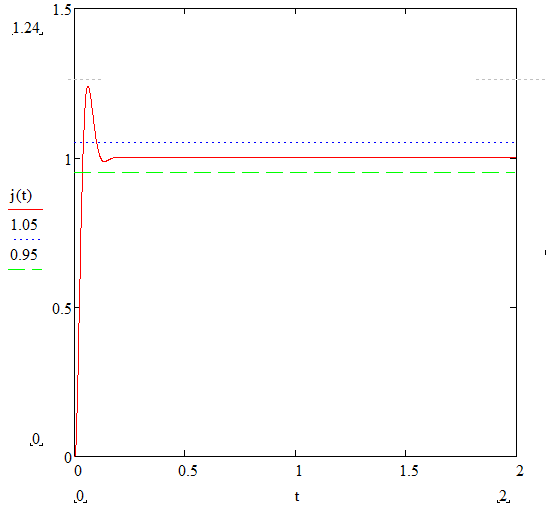
Рисунок 24 – Построение переходной характеристики с коэффициентом Кд, удовлетворяющим ТЗ
2) t≈0.1c
2) Получение переходной характеристики и построение графика системы, не соответствующей ТЗ.
Рисунок 25 – Построение переходной характеристики с коэффициентом Кд, не удовлетворяющим ТЗ
t≈0.09c
Приложение F
Проверка системы, полученной по методу ЛАЧХ, по прямым показателям качества
I) Проверка неупрощенной системы
Получение переходной характеристики
Рисунок 26 – Построение переходной характеристики скорректированной неупрощенной системы
По полученной характеристике определим:
t=0.2c
II) Проверка упрощенной системы
Получение переходной характеристики
Рисунок 27 – Построение переходной характеристики скорректированной упрощенной системы
По полученной характеристике определим:
t=0.18 c
Приложение G
Оценка показателя колебательности
Получение модуля передаточной функции по выходу ДОС
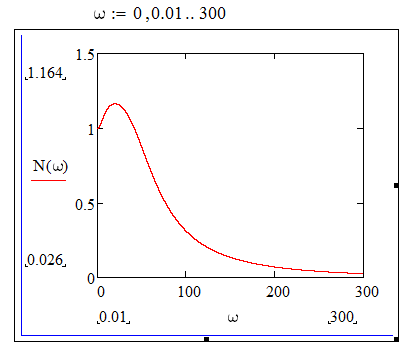
Рисунок 28 – Построение АЧХ системы
Приложение H
Оценка прямых показателей качества по ВЧХ
Рисунок 29 – Построение ВЧХ системы
Так как ВЧХ имеет положительный и отрицательный экстремумы, то перерегулирование можно оценить по формуле:
Определим частоту положительности:
P(ωп)=0.5Р(0)
Рисунок 30 – Определение частоты положительности
ωп=33.45 Гц
Приложение I
Построение ПФ по выходу ОУ и ДОС.
Построение графиков переходных функций
1) Переходная функция по выходу ОУ:
2) Переходная функция по выходу ДОС:
Определим прямые показатели качества
1) Прямые показатели качества по выходу ОУ:
· перерегулирование:
· время регулирования:
t=0.178 c.
2) Прямые показатели качества по выходу ДОС:
Эти показатели определены в приложении Е.
t=0.180 c.
Приложение J
Определение величины Хо по выходу УМ.
Рисунок 31 – Построение переходной характеристики по выходу УМ
hум max=2081
Приложение K
Определение частоты ω0
Рисунок 32 – Определение ω0 по АЧХ
ω0=20.5 Гц
