Структурная схема замкнутой системы управления представлена на рисунке 4.
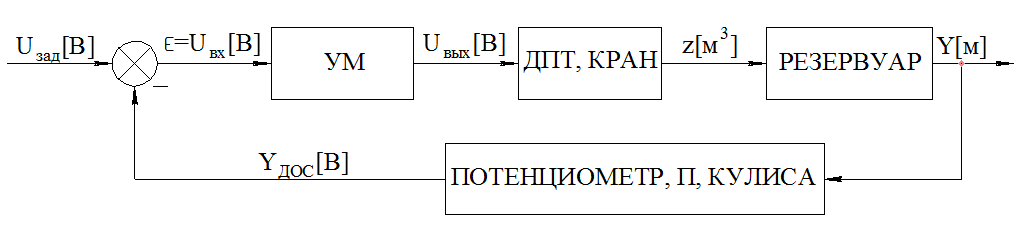
Рисунок 4 – Структурная схема замкнутой системы управления
Передаточные функции ОУ, ИМ и ДОС считаются известными:
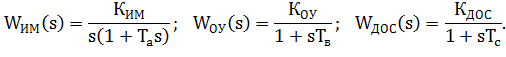
Параметры: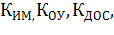 
Ta, Tb, Tc заданы в техническом задании.
Определим размерности всех параметров системы:
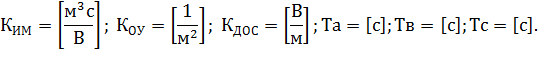
УПЭ (УМ) предполагается безынерционным, но с ограниченной зоной линейности. Статическая характеристика УПЭ представлена на рисунке 5.
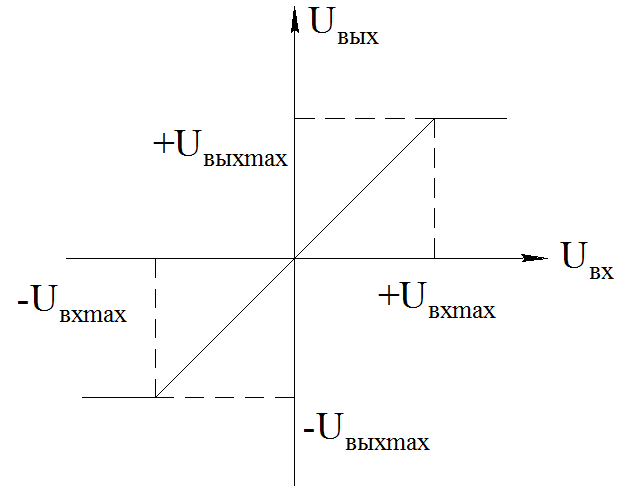
Рисунок 5 – Статическая характеристика УПЭ
Параметры: Uвхmax, Uвыхmax заданы в техническом задании.
На начальном этапе исследования воспользуемся линеаризацией на физическом уровне: будем считать, что усилитель мощности имеет неограниченную зону линейности. Мы можем принять это допущение, так как в процессе работы УПЭ, его выходная величина меняется в небольшом диапазоне (±4В) по линейному закону. Структурная схема линеаризованной системы представлена на рисунке 6.
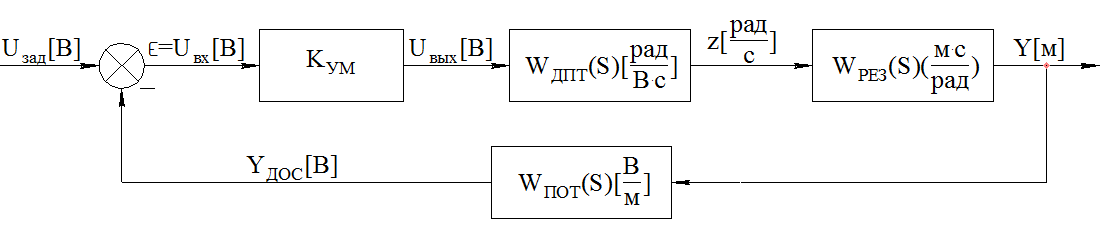
Рисунок 6 – Структурная схема линеаризованной системы
Анализ устойчивости исходной линеаризованной системы по алгебраическому критерию
Коэффициент усилителя мощности найдем из характеристики, указанной на рисунке 5, для линейной зоны усиления:
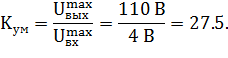
Для проверки линеаризованной системы по алгебраическому критерию, необходимо записать характеристическое уравнение замкнутой системы. Это уравнение имеет вид:
1+Wp(s)=0. (1)
где
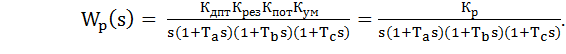(2)
С помощью программного пакета MathCad, преобразуем
характеристическое уравнение (рисунок 7):
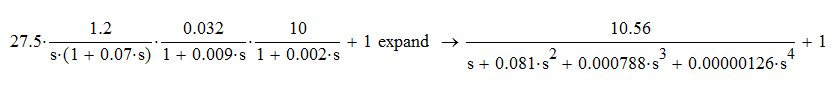
Рисунок 7 – Преобразование ХУ ЗС
Окончательный вид ХУ ЗС:
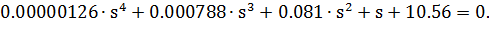(3)
Так как общий вид ХУ ЗС имеет вид:
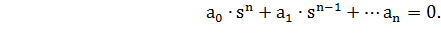(4)
то запишем коэффициенты ХУ ЗС:
· а0=0.00000126;
· а1=0.000788;
· а2=0.081;
· а3=1;
· а4=10.56.
Полученная система – 4-го порядка. Для проверки системы по критерию Гурвица, необходимо проверить ее на выполнение необходимого и достаточного условия устойчивости.
Необходимое условие: аi>0. Это условие выполняется.
Достаточное условие: все определители Гурвица должны быть положительными. Так как система 4-го порядка, то достаточно проверить, положителен ли определитель 3-го порядка. Это следует из-за того, что определитель 4-го порядка равен произведению диагонального минора Δ3 на коэффициент а4. Так как этот коэффициент, вследствие выполнения необходимого условия устойчивости, положителен, то при записи неравенства его можно опустить.
В итоге, требуется проверить, выполняется ли условие:
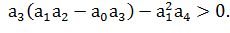(5)
После подстановки численных значений, получим:
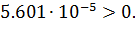
Достаточное условие выполняется, следовательно, замкнутая система устойчива.
