1) Определение запасов устойчивости системы:
Запасы устойчивости будем проверять по ЛЧХ системы, выполненной ниже. Правило определения запасов устойчивости: запас по фазе Δφ отсчитывается по ЛФХ на частоте среза wс, а запас по амплитуде Lh соответствует значению ЛАХ на критической частоте wкр, взятому с обратным знаком.
Расчет выполним в MathCad (рисунок 10):
Рисунок 10 – Построение ЛХЧ скорректированной системы
Проведем расчет значений:
Получим значения: запас по амплитуде Lh = 16.8 дБ; запас по фазе Δφ= =35.68̊.
2) Оценка показателя колебательности:
Показатель колебательности М, представляет собой резонансное значение амплитудно-частотной характеристики замкнутой системы в относительных единицах, т.е. отношение максимальной амплитуды АЧХ к начальной ординате.
Показатель колебательности характеризует склонность систем или объектов к колебательности. Чем выше показатель колебательности, тем более колебательна система, то есть менее качественна.
Для определения этого показателя необходимо построить график АЧХ (график зависимости модуля частотной передаточной функции от частоты) и по снятым с графика значениям, определить значение показателя колебательности.
Расчет этого показателя приведен в приложении G.
По результатам проведенных расчетов, были получены численные значения параметров:
М=1.164.
Считается, что значение показателя колебательности, обеспечивающего малую колебательность системы, лежит в пределах:
1.1<М<1.3.
Полученный нами показатель укладывается в этот диапазон, следовательно, система обладает хорошими показателями по качеству.
3) Оценка прямых показателей качества по ВЧХ «вход-выход ДОС»
По ВЧХ замкнутой системы, можно определить диапазон значений прямых показателей качества системы.
Расчет этих показателей приведен в приложении H.
По результатам расчетов видно, что перерегулирование менее 20.403%. Так как ранее мы получили значение перерегулирования 17.8%, то расчет проведен
верно(полученное значение входит в диапазон).
Для оценки времени регулирования воспользуемся неравенством:
где ωп – частота положительности.
Определив ωп в приложении Е, оценим диапазон времени регулирования:
.
Так как ранее мы получили значение времени регулирования 0.18 с, то расчет проведен верно (полученное значение входит в диапазон).
4) Оценка прямых показателей качества по нулям и полюсам передаточной функции замкнутой системы (корневые оценки показателей)
Оценку прямых показателей качества системы можно произвести на базе корневых показателей. Корневые показатели качества САР основаны на значениях нулей и полюсов ПФ, их расположении на комплексной плоскости. Основными корневыми показателями качества являются:
1) Степень устойчивости η – абсолютное значение действительной части ближайшего к мнимой оси полюса ПФ рассматриваемой системы. Степень устойчивости применяется для оценки быстродействия системы, т.е. времени регулирования.
2) Коэффициент колебательности μ – максимальное отношение мнимой части комплексного корня характеристического уравнения системы к действительной части. Коэффициент колебательности является оценкой запаса устойчивости системы и характеризует склонность системы к колебательным переходным процессам. Эти же свойства оценивает прямой показатель качества – перерегулирование.
Определим нули и полюса нашей функции.
Знаменатель передаточной функции соответствует характеристическому уравнению системы. Его корни – полюса передаточной функции. Нули передаточной функции - корни многочлена числителя.
Получим характеристическое уравнение замкнутой системы и найдем его корни:
Рисунок 11 – Нахождение полюсов ПФ
Уравнение для нулей ПФ замкнутой системы:
12.672s+105.6=0.
Определим степень устойчивости и коэффициент колебательности:
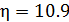
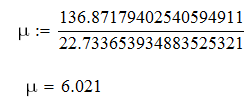
По величине 
оценим время регулирования, так как ближайшему к мнимой оси полюсу соответствует составляющая регулируемой величины, затухающей наиболее медленно:
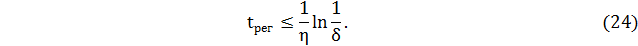
Примем 
,и проведем расчет:
По величине 
оценим перерегулирование:
Истинные значения перерегулирования и времени регулирования удовлетворяют полученным диапазонам.
Полученные оценки по корневому методу и по ВЧХ системы дают очень широкий диапазон значений прямых показателей и точные значения никогда не будут известны.
