Резервирование, при котором возможно восстановление отказавших элементов, является эффективным средством повышения надежности. Отказ резервированной группы с восстановлением произойдет, если все элементы, составляющие группу, ремонтируются.
При резервировании с восстановлением резерв как бы все время пополняется восстанавливаемыми блоками.
Показатели надежности, как правило, определяются при условии, что в момент включения все элементы работоспособны.
Наиболее часто используются два метода расчета надежности восстанавливаемых систем, которые условно называются: метод интегральных уравнений и метод дифференциальных уравнений.
Будем рассматривать в дальнейшем 2-ой метод. В методе дифференциальных уравнений использовано допущение о показательных распределениях времени между отказами и времени восстановления.
Вначале перечисляются возможные состояния системы и составляется ее математическая (логическая) модель в виде схемы состояний, на которой прямоугольниками или кружками изображаются возможные состояния и стрелками возможные направления переходов из одного состояния в другое. По схеме состояний составляют систему дифференциальных уравнений для вероятностей состояний.
Для этого целесообразно использовать следующие правила:
- левые части уравнений содержат производные по времени вероятностей соответствующих состояний 
, а каждый член правой части уравнения получается путем умножения интенсивности перехода, стоящей над стрелкой, связанной с данным состоянием, на соответствующую вероятность состояния;
- знак зависит от направления стрелки (плюс, если стрелка направлена острием к состоянию, и минус в противном случае);
- число уравнений равно числу состояний; система дифференциальных уравнений должна быть дополнена нормировочным условием, состоящим в том, что сумма вероятностей всех состояний равна единице.
Решение системы дифференциальных уравнений с помощью преобразований Лапласа позволяет определить требуемые показатели надежности.
Когда перерывы в работе системы допустимы, в качестве показателей надежности используют функцию готовности Кг(t) и функцию простоя Kп(t) или коэффициенты готовности Kг и простоя Кп определяемые в виде
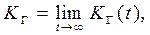
| (3.1) |
|
Функция готовности Kг (t) равна по определению вероятности того, что в момент времени t система исправна. Функция простоя К п(t) равна вероятности того, что в момент времени t система неисправна.
Имеют место соотношения
| Кг(t)+Kп(t)= 1; | (3.2) |
| Кг+Кп= 1. |
Часто рассматривают установивший режим эксплуатации при t ®¥. Тогда 
и система дифференциальных уравнений переходят в систему алгебраических уравнений.
Когда перерывы в работе системы недопустимы, в качестве показателей надежности используются условные вероятности непрерывной безотказной работы в течение заданного времени выполнения задачи 
при условии, что в начальный момент времени все элементы системы работоспособны. В рассматриваемом случае имеются “поглощающие” состояния и необходимо решить полную систему дифференциальных уравнений при соответствующих начальных условиях.
При нескольких работоспособных состояниях
| (3.3) |
где n - число работоспособных состояний; Pj (t) - вероятность j -го работоспособного состояния.
Часто число неработоспособных состояний значительно меньше числа работоспособных или всего одно. При этом удобнее вычислять коэффициент простоя
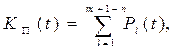
| (3.4) |
где Pl (t) -вероятность l- го неработоспособного состояния; m+1 - общее число состояний.
Особенности расчета резервированных систем
Система, состоящая из равнодежных одного основного и k резервных элементов, может находиться в любом из (k +2) состояний:
0 - все элементы работоспособны;
1- один элемент в неработоспособном состоянии;
j - когда j элементов в неработоспособном состоянии;
k+1 - когда (k+1) элементов в неработоспособном состоянии.
Предполагается, что при замене работающего элемента на резервный перерыва в работе системы не происходит, поэтому отказ системы наступает при одновременной неработоспособности основного и всех резервных элементов (состояние k+1).
Важным показателем является среднее время безотказной работы
| (3.5) |
При решении системы уравнений, составленных по схеме состояний с помощью преобразований Лапласа, целесообразно использовать правило, облегчающее расчет.
Для определения среднего времени безотказной работы достаточно найти преобразование Лапласа вероятности безотказной работы P (s) и подставить в него s= 0.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Изучить теоретические положения по расчету количественных показателей надежности восстанавливаемых систем с резервированием элементов.
2. Решить задачу, приведенную ниже, в соответствии с заданным вариантом.
Задание для лабораторной работы
Задача. Радиоприемное устройство, состоящее из рабочего блока и блока в нагруженном резерве, рассчитано на непрерывную круглосуточную работу. Интенсивность отказов и восстановления каждого блока равныl; m (см. табл. 3.1). Имеются две дежурные ремонтные бригады. Определить вероятность застать радиоприемное устройство в неработоспособном состоянии через 3 часа, 30 часов, 300 часов после включения (значение функции простоя) и значение коэффициента простоя. Для проверки правильности результата определить коэффициент простоя для установившегося режима.
Таблица 3.1. Значение параметров λ и m для задачи
| № Варианта | ||||||||||
| λ∙10-3, 1/ч | 6,2 | 7,3 | 5,6 | 9,4 | 7,4 | 4,1 | 4,2 | 6,9 | 1,7 | 5,3 |
| m∙10-1, 1/ч | 2,6 | 3,7 | 6,5 | 4,9 | 4,7 | 1,4 | 2,4 | 9,6 | 7,1 | 3,5 |
| № Варианта | ||||||||||
| λ∙10-3, 1/ч | 7,5 | 9,9 | 5,7 | 3,8 | 3,9 | 7,2 | 8,7 | 7,1 | 3,1 | |
| m∙10-1, 1/ч | 5,7 | 9,9 | 7,5 | 8,3 | 9,3 | 2,7 | 7,8 | 1,7 | 1,3 | |
| № Варианта | ||||||||||
| λ∙10-3, 1/ч | 7,6 | 6,4 | 6,1 | 6,8 | 7,9 | 2,6 | 8,1 | 5,5 | 8,2 | |
| m∙10-1, 1/ч | 6,7 | 4,6 | 1,6 | 8,6 | 9,7 | 6,2 | 1,8 | 5,5 | 2,8 |
3. Оформить и защитить отчет по лабораторной работе.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Каков порядок построения графа состояний системы
2. Как по заданному графу состояний системы построить систему дифференциальных уравнений, описывающих характеристики надежности?
3. Что такое коэффициент готовности?
4. Как определяется коэффициент готовности?
5. Как определяется функция готовности?
6. Как определяется функция простоя?
7. Как определяется вероятность безотказной работы?
8. Как определяется средняя наработка на отказ?
ЛАБОРАТОРНАЯ РАБОТА №4
Анализ показателей надежности по статистическим данным:
построение гистограмм, проверка допустимости закона распределения на основе критерия согласия, расчет точечных и интервальных оценок показателей надежности
Цель работы – приобретение практических навыков построения гистограмм для интенсивности отказов и вероятности безотказной работы по статистическим данным об отказах изделия; проверки допустимости экспоненциального закона надежности для периода нормальной эксплуатации на основе критерия согласия Колмогорова; расчета точечной и интервальной оценки времени наработки до первого отказа
