Время между соседними отказами объекта является непрерывной случайной величиной. Эта случайная величина с вероятностной точки зрения будет полностью определена, если известна ее функция распределения.
Случайные величины в зависимости от их физического смысла могут иметь различные законы распределения. В теории вероятностей известно большое число таких законов. Однако рассматривать количественные характеристики надежности имеет смысл только для ограниченного их числа. При изучении надежности технических систем наиболее часто применяют законы распределения: экспоненциальный, нормальный, Рэлея, Вейбулла.
Принятый для конкретного объекта закон распределения является лишь математической моделью его истинного закона распределения. Одной из основных задач теории надежности является выявление и математическое описание истинного закона распределения с возможно наибольшей степенью точности. Для решения этой задачи необходимо для каждого периода (приработки, нормальной эксплуатации или старения) работы объекта подобрать как закон распределения, так и его параметры.
Наиболее распространенным законом распределения является экспоненциальный закон. При экспоненциальном законе распределения времени возникновения отказов интенсивность отказов является величиной постоянной. Это условие приблизительно реализуется в период нормальной эксплуатации объекта, если исключить период приработки и период интенсивного старения. Тогда зависимости между основными количественными характеристиками надежности будут выражены формулами:
 ; ;
| (1.1) |
 ; ;
| (1.2) |
 ; ;
| (1.3) |
 ; ;
| (1.4) |
Графики основных количественных характеристик надежности для экспоненциального закона приведены на рис. 1.1.
В отличие от экспоненциального нормальное распределение используют для описания таких систем и их элементов, которые подвержены действию износа, т.е. в период старения. При этом основные количественные характеристики будут выражены следующим формулами:
 ; ;
| (1.5) |
 ; ;
| (1.6) |
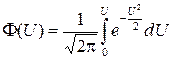 ; ;
| (1.7) |
 ; ;
| (1.8) |
 ; ;
| (1.9) |
 ; ;
| (1.10) |
где Ф(U) – нормированная функция Лапласа, обладающая свойствами
| Ф(0) = 0; | (1.11) |
| Ф(– U) = –Ф(U); | (1.12) |
| Ф(¥) = 0,5 | (1.13) |
здесь
mt – среднее значение случайной величины Т;
s t 2– дисперсия случайной величины Т;
Т – время безотказной работы изделия.
Значения функции Лапласа и функции j(U) приводятся в приложениях в учебных пособиях и сборниках задач по теории вероятности и математической статистике или учебных пособиях и сборниках задач по теории надежности.
Графики основных количественных характеристик надежности для нормального закона приведены на рисунке 1.2.

| 
|
| Рисунок 1.1. Экспоненциальный закон распределения | Рисунок 1.2. Нормальный закон распределения |
При распределении Вейбулла основные количественные характеристики рассчитываются по следующим формулам:
  ; ;
| (1.14) |
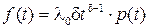 ; ;
| (1.15) |
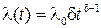 ; ;
| (1.16) |
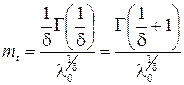 ; ;
| (1.17) |
где λ0, δ – параметры закона распределения Вейбулла. Г(x) – гамма-функция, значения которой приводятся в приложениях учебных пособий по теории вероятности и математической статистике или теории надежности.

| 
|
| а) | б) |
Рисунок 1.3. Закон распределения Вейбулла а) при δ<1, б) при δ>1.
Это двухпараметрическое распределение. При δ=1 распределение Вейбулла совпадает с экспоненциальным (рис. 1.1), когда интенсивность отказов постоянна, что характерно для периода нормальной эксплуатации; при δ < 1 интенсивность отказов монотонно убывает (рис. 1.3 а), что свойственно периоду приработки, при δ > 1 монотонно возрастает (рис. 1.3 б), что соответствует периоду старения. Таким образом, закон распределения Вейбулла можно использовать для описания распределения времени до отказа систем включая периоды приработки, нормальной эксплуатации и старения элементов.
При δ = 2 закон Вейбулла переходит в закон Рэлея, который может быть применен для описания характеристик надежности в период интенсивного износа для некоторых технических устройств. Количественные характеристики надежности в законе Рэлея задаются формулами
 ; ;
| (1.18) |
 ; ;
| (1.19) |
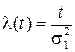 ; ; 
| (1.20) |
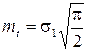 , ,
| (1.20) |
где s1 – мода распределения случайной величины Т;
Т – время безотказной работы изделия.
Поведение характеристик надежности качественно совпадает с законом Вейбулла при δ > 1, что показано на рис. 1.3 б.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Изучить теоретические положения по расчету надежности элементов, отказы которых подчинены различным законам распределения. Ознакомиться с формулами для вычисления количественных показателей надежности при известных законах распределения.
2. Получить допуск для выполнения лабораторной работы.
3. Решить задачи 1, 2, 3 и 4 приведенные ниже в соответствии с заданным вариантом.






