Задача 1. Дана система, схема расчета надежности которой изображена на рисунке 2.1. Известно, что все элементы системы равнонадежны. Необходимо найти вероятность безотказной работы системы. Значение вероятностей безотказной работы элементов приведены в табл. 2.1.
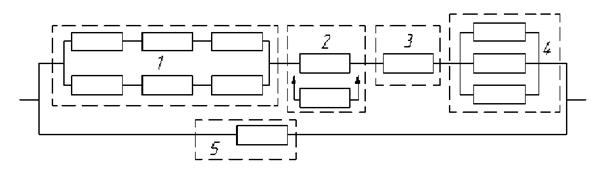
Рис. 2.1. Схема расчета надежности
Таблица 2.1. Исходные данные для задачи 1
| № варианта | ||||||||||
| P | 0,69 | 0,68 | 0,67 | 0,96 | 0,95 | 0,94 | 0,93 | 0,92 | 0,91 | 0,9 |
| № варианта | ||||||||||
| P | 0,89 | 0,88 | 0,87 | 0,86 | 0,85 | 0,84 | 0,83 | 0,82 | 0,81 | 0,8 |
| № варианта | ||||||||||
| P | 0,79 | 0,78 | 0,77 | 0,76 | 0,75 | 0,74 | 0,73 | 0,72 | 0,71 | 0,7 |
Задача 2. Найти вероятность безотказной работы системы в момент времени 1000 часов, схема расчета надежности которой изображена на рис. 2.1. Значения интенсивности отказов элементов λ·10-5 ч-1 приведены в табл. 2.2.
Таблица 2.2. Значения интенсивности отказов для элементов каждого блока
| № варианта | ||||||||||
| Для блока 1 | ||||||||||
| Для блока 2 | ||||||||||
| Для блока 3 | ||||||||||
| Для блока 4 | ||||||||||
| Для блока 5 |
Таблица 2.2. Продолжение
| № варианта | ||||||||||
| Для блока 1 | ||||||||||
| Для блока 2 | ||||||||||
| Для блока 3 | ||||||||||
| Для блока 4 | ||||||||||
| Для блока 5 | ||||||||||
| № варианта | ||||||||||
| Для блока 1 | ||||||||||
| Для блока 2 | ||||||||||
| Для блока 3 | ||||||||||
| Для блока 4 | ||||||||||
| Для блока 5 |
Задача 3. Система состоит из N равнонадежных элементов, средняя наработка до отказа элемента Т. Предполагается, что справедлив экспоненциальный закон надежности для элементов системы. Основная и резервная системы равнонадежны. Необходимо найти среднюю наработку до отказа Тс системы и вероятность безотказной работы системы Рс в момент времени 100 ч в следующих случаях:
а) нерезервированной системы;
б) дублированной системы при постоянно включенном резерве;
в) дублированной системы при включении резерва по способу замещения.
Таблица 2.3. Исходные данные для задачи 3
| № варианта | ||||||
| N | ||||||
| Т, ч | ||||||
| № варианта | ||||||
| N | ||||||
| Т,ч | ||||||
| № варианта | ||||||
| N | ||||||
| Т, ч | ||||||
| № варианта | ||||||
| N | ||||||
| Т, ч | ||||||
| № варианта | ||||||
| N | ||||||
| Т, ч |
3. Оформить и защитить отчет по лабораторной работе.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что такое постоянное резервирование элементов?
2. Что такое резервирование замещением?
3. В каком состоянии могут находиться элементы при резервировании замещением?
4. Что такое общее резервирование?
5. Что такое раздельное резервирование?
6. Что такое скользящее резервирование?
7. Чему равна вероятность отказа системы с постоянным резервом и с целой кратностью?
ЛАБОРАТОРНАЯ РАБОТА №3
Расчет показателей надежности резервированных устройств с учетом восстановления. Определение функций готовности и простоя и коэффициентов готовности и простоя
Цель работы – приобретение практических навыков вычисления количественных показателей надежности систем с резервированием элементов с учетом их восстановления.






