Так як Ipq=Ip*Iq, то
 Ipq=
Ipq= 
 *
*  (6)
(6)
(7)
Формула (6) являє собою систему співзалежних індексів, вираз (7) — побудований на ній індексний факторний аналіз. Останній показує, що загальна абсолютна зміна товарообігу дорівнює його зміні за рахунок кількості реалізованих товарів плюс зміна товарообігу за рахунок зміни цін.
Число факторів може бути і більшим, система індексів будується аналогічно шляхом послідовної заміни «О» на «1» в чисельнику і знаменнику. Наприклад індекс вартості матеріалу на виробництво різних виробів, кожний з яких виробляється з одного певного матеріалу, будується таким шляхом.
Позначимо: а — кількість виробів певного виду; b -витрата матеріалу на одиницю продукції; с — ціна за одиницю матеріалу.
Загальну вартість можна було б позначити як
R =  аЬс.
аЬс.
Тоді умовно представимо
Iabc=Ia*Ib*Ic= 

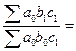
 (8)
(8)
Неважко побачили логіку\переходу від (6).до (8). Таке спрощене позначення величин через а, Ь, с при індексному факторному аналізі поширене в літературі. Весь комплекс факторів, які визначають результати роботи підприємства, можна розділити на економічні та соціальні. Звичайно провести аналіз впливу економічних складових не викликає особливих труднощів. Основою побудови індексної моделі є ланцюгова схема зв'язку, в якій залежний фактор у є функція деякої множини факторів хij [9]:
y = 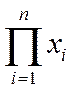 (9)
(9)
Аналіз впливу окремих факторів на динаміку зміни прибутку виконується в рамках надійної системи. В основі побудови лежить послідовність включення факторів у систему та черговість їх вивчення. Встановлення строго визначеної послідовності факторів - основне завдання даного аналізу. Воно розв'язується послідовним розширенням вихідної моделі. Характерною рисою багатофакторної моделі є послідовний взаємозв'язок факторів, що входять до даної моделі, — чисельник розрахункової формули одного з них одночасно є знаменником розрахункової формули іншого.
| Таблиця 7.2 | |||
| № п/п | Показники | Розрахунки | позначення |
| Чистий прибуток | ЧП | ||
| Собівартість реалізованої продукції | В | ||
| Об'єм реалізації | QP | ||
| Обсяг випуску | Qв | ||
| Середньорічна вартість ОФ | ОФ | ||
| 6, | Чисельність працівників | Т | |
| Рівень рентабельності | 
| Р | |
| Рентабельність реалізації | 
| Х1 | |
| Коефіцієнт реалізації | 
| X2 | |
| Фондовіддача | 
| X3 | |
| Фондоозброєність | 
| Х4 | |
| Трудомісткість | 
| X5 | |
| Обсяг випуску на одиницю витрат | 
| Х6 |
Схематично це можна подати таким чином:

Для зручності подальших розрахунків введемо позначення у вигляді табл. 7.2
Загальну рентабельність можна подати таким чином:
 =
=  *
*  *
*  *
*  *
*  *
*  (10)
(10)
Тоді зміна рівня рентабельності (у) буде мати вигляд:
а) під впливом всіх факторів
Iy=  (11)
(11)
б) під впливом зміни рентабельності реалізації
Ix1=  (12)
(12)
в) під впливом зміни коефіцієнта реалізації
Ix2=  (13)
(13)
г) під впливом зміни фондовіддачі
Ix3= 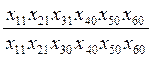 (14)
(14)
д) за рахунок зміни фондоозброєності
Ix4= 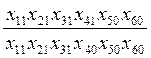 (15)
(15)
е) під впливом зміни трудомісткості або продуктивності (ґ = 1/w). Ці показники мають обернений зв'язок
Ix5=  (16)
(16)
ж) при зміні рівня витрат
Ix6=  (17)
(17)
На основі індексної моделі можна розкласти абсолютний приріст рентабельності за факторами:



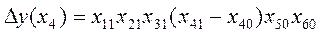


Для цієї ж мети можна використовувати інший більш компактний метод розрахунку, в основі якого лежить базисний рівень рентабельності, відкорегова-ний на індекси включених у модель факторів, при послідовному множенні якого відповідно до ланцюгової схеми зв'язку базисного рівня рентабельності на індивідуальні індекси факторів отримують розрахункові значення, які прийняв би змодельований показник під впливом і-го фактора та при незмінному рівні інших, включених у модель.
Позначивши базисне значення рентабельності через y, розрахункове значення рентабельності для першого фактора через у1, для другого — у2, і т. д., то порядок визначення абсолютного впливу виглядає таким чином:
y1= Ix1*y0
y2= Ix2*y1
y3= Ix3*y2
………….
Y6= Ix6*y5
У загальному вигляді розрахунок має вигляд:
 (18)
(18)
Застосовуючи такий метод, можна тим самим виміряти, в якій мірі вплинув кожний із факторів на загальні зміни рівня рентабельності, та, виходячи з цього, можна визначити міру цього впливу в процентах. Наявність знака «—» буде вказувати на обернений вплив.
dxi =  (19)
(19)
Якщо виникає необхідність провести аналіз впливу факторів для декількох об'єктів одразу ж (наприклад, підприємств однієї галузі), то в чисельнику та знаменнику відповідних формул (11—17) буде розраховувати- > ся сума добутків по декількох об'єктах та абсолютний приріст. За рахунок кожного фактора можна розрахувати різницю між чисельником та знаменником відповідного індекса.
Індекси середніх величин.
Якщо вивчається динаміка середніх величин, то використовують загальні індекси середніх величин.
Розглянемо їх на прикладі індексу середньої урожайності двох зернових культур: пшениці та гречки.
Як відомо, урожайність - це збір культури з одиниці площі: У = ВЗ/П, де ВЗ -валовий збір; П -розмір посівної площі. Тоді індивідуальний індекс урожайності, який характеризує динаміку урожайності окремої культури, обчислюється за формулою
iY = 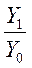
Загальний індекс характеризує динаміку середньої урожайності зернових

Цей індекс має назву індексу змінного складу; його величина залежить від двох факторів: зміни усередненого показника (в даному випадку врожайності) та зміни структури сукупності (співвідношення, питомої ваги площ під окремими культурами).
Для того щоб показати, як змінилась середня урожайність під впливом кожного фактора в окремості, обчислюють відповідно ще два індекси: індекс фіксованого складу та індекс впливу структурнихзрушень:


Очевидно, I  -можна записати у формі, що має назву агрегатної
-можна записати у формі, що має назву агрегатної

Якщо сам індекс показує зміну урожайності, То різниця між чисельником і знаменником його агрегатної форми показує зміну валового збору за рахунок зміни урожайності окремих культур.
Якщо на зміну середньої урожайності впливають два фактори, то на зміну валового збору — до того ж і третій — розмір посівної площі.
Приклад 7.3
Маємо дані про роботу двох шахт, які утворюють собою трест, за 1992 та 1993 pp. (табл. 7.3). Необхідно обчислити індивідуальні та загальні індекси продуктивності праці, загальний приріст видобутку вугілля та приріст за рахунок окремих факторів.
| Таблиця 7.3 | ||||||||
| № шахта | Видобуток вугілля, тисіт | Відпрацьовано людино-днів | Продуктивність праці т/л-дн | Частка у витрата, праці | ||||
| q0 | q1 | Т0 | Ті | We | Wi | d0 | di | |
| 2.0 | 2.2 | 0.4 | 0.67 | |||||
| 30.6 | ЗО | 1.5 | 1.53 | 0.6 | 0.33 | |||
| Разом | 118.6 | 1.7 | 1.997 | 1.0 | 1.00 |
Добудуємо таблицю та обчислимо підсумковий рядок. Продуктивність праці -- це видобуток вугілля за одиницю часу. Для шахти №1: Wt = 88000:40000 = 2,2 т/л-дн; W0 = 40000:20000 = 2,0 т/л-дн.
Отже, індивідуальний індекс продуктивності праці становить для шахти №1 — 1,1 (2,2/2,0), для шахти №2 - 1,02 (1,53/1,5) (табл. 7.4).
Таблиця 7.4 Таблиця розрахунків індексів середньої продуктивності праці
| № шахти | Iw | |
| 1,1 | ||
| 1,02 |
Таким чином, продуктивність праці у першій шахті зросла в 1,1 раза, або на 10%. Важливо підкреслити, що цей індекс ми називаємо і ндивідуальним, бо він відноситься до одиниці сукупності — шахти№1
Але зрозуміло, що вік, з іншого боку, характеризує зміну середньої продуктивності праці всіх шахтарів шахти №1, тобто сукупності. Аналогічно для другої шахти. Але якщо продуктивність праці на одній шахті зросла на 10%, а на другій - на 2%, то це зовсім не обов'язково, що в цілому по тресту вона зросла на 6%. Обчислимо загальний індекс продуктивності:
I  (116.3%)
(116.3%)
Виявляється, що продуктивність праці по тресту збільшилась на 16,3%, тобто ще в більшій мірі, ніж на кращій у цьому відношенні шахті.
Замість цього прикладу ми могли б запропонувати десятки інших. Хоч такий, в якому середня заробітна плата в колективі збільшилась у той час, коли одна! частина його в травні заробила тіж гроші, що в квітні, І а друга — навіть менші. На жаль завжди знайдуться такі, що не розуміють причин цього, що не зуміють правильно зрозуміти інформацію про середній рівень заробітної плати, споживання на душу населення, радіаційного забруднення тощо. Але інформацію про І зміну цих середніх, які хоч і є абстрактними, може [ торкнутись кожного з нас дуже конкретно.
Таким чином Iзс може виходити за межі індиві-| дуальних індексів. У нашому прикладі він показує І зміну середньої продуктивності за рахунок зміни продуктивності по кожній з шахт, а також за рахунок змін в структурі витрат часу.
Для того щоб визначити вплив першого фактору, обчислимо індекс фіксованого складу:
I 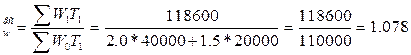
 (107,8%).
(107,8%).
На відміну від Iзс, IФС ніколи не виходить за межі індивідуальних індексів.
Поглянемо на табл. 7.3 з обчисленими даними. Легко помітити, що: продуктивність праці на першій шахті була вищою в кожному році; частка відпрацьованого на ній часу (а, як бачимо, використовується він більш ефективно, ніж на другій) різко збільшилась і стала більшою, ніж частка другої (67% проти 33%).
Ці зміни в структурі відпрацьованого часу позитивно позначились на зміні середньої продуктивності:
I 

Тепер визначимо зміну видобутку вугілля по тресту — загальну і за рахунок окремих факторів:
 = 118600-85000 = 33600 т.
= 118600-85000 = 33600 т.
Фактори, які впливають на зміну загального видобутку вугілля, можуть бути різними, але в кінці кінців їх можна звести до двох: продуктивності праці та загальних витрат відпрацьованого часу:
 = (1,977 -1,7) • 60000 = 16600 т;
= (1,977 -1,7) • 60000 = 16600 т;
 = (60000 - 50000) • 1,7 = 17000 т.
= (60000 - 50000) • 1,7 = 17000 т.
Перевіримо:
 =6600 +17000 = 33600 т.
=6600 +17000 = 33600 т.






