Характеристики рядів динаміки

Однією із узагальнюючих характеристик рядів динаміки є середній рівень. У періодичному ряді він обчислюється як проста середня арифметична:

де у_i — рівні ряду; n — число рівнів ряду.

У моментному ряду з рівними відрізками часу об­числюється як середня хронологічна:

Якщо відрізки часу між моментами різні, то вико­ристовують формулу середньої арифметичної зваже­ної:

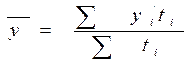
Де

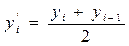
де у_i — середні рівні окремих інтервалів часу; t_i — тривалість відповідних інтервалів.

Для опису рядів динаміки використовується також система взаємозв'язаних характеристик: абсолютний приріст, темп зростання, темп приросту і абсолютне значення одного проценту приросту. Обчислення ха­рактеристик грунтується на співставленні рівнів ряду.

Якщо базою при цьому є попередній рівень, то во­на називається змінною, а самі характеристики — лан­цюговими. Якщо ж за базу обраний початковий рівень у„, то базу називають постійною, а характеристики ба­зисними.

Абсолютный приріст характеризує розмір збільшення (зменшення) рівня ряду за певний період.

Вони можуть бути обчислені як ланцюгові, так і базисні:

ланцюговий:

= у_t – у_t-1;

базисний:

= у_t – у₀;

 

 

Де y_t - рівень відносно конкретного моменту або інтервалу часу t_n, у₀ — базисний рівень.

Середній абсолютний приріст:

 

де n — число ланцюгових абсолютних приростів,

у_к —кінцевий рівень ряду.

Темп зростання (t) показує, в скільки разів один рівень ряду динаміки більший за другий, об­числюється в коефіцієнтах або процентах:

а) ланцюговий

t_t =

б) базисний

t_t =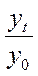

 

Темп приросту — це відношення абсолютного приросту до попереднього або початкового рівня, або

T = t- 1,

він теж може бути ланцюговим та базисним залежно від t.

Для характеристики темпів зростання та приростів за весь період, охоплений рядом динаміки, обчислю­ють середній темп зростання та темп приросту. Се­редній темп зростання обчислюється за формулою

де у₀ - початковий рівень;

у_n — кінцевий рівень;

n — число членів ряду;

— кінцевий базисний темп росту.

Якщо абсолютні дані динамічного ряду відсутні, то середній коефіцієнт можна обчислити на основі лан­цюгових коефіцієнтів.

 

n— число ланцюгових темпів зростання.

Для знаходження середньої із середніх темпів зро. стання за неоднакові інтервали часу використовують середню геометричну зважену

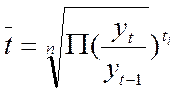
де t_i- тривалість відрізків часу.

Наприклад, середньорічний темп зростання обсягу продукції за три роки становив 1,07, а за наступні два - 1,10. Тоді середньорічний темп зростання обсягу продукції за всі п'ять років становив

Характеристики рядів динаміки пов'язані між со­бою таким чином.

1) Сума абсолютних ланцюгових приростів до­рівнює загальному приросту за весь період:

де — ланцюгові абсолютні прирости, — кін­цевий базисний абсолютний приріст.

2) Добуток ланцюгових темпів зростання дорівнює кінцевому базисному:

t₁t₂…t_n = t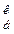

3) 3 темпами приросту арифметичні дії не прово­дяться.

При порівнянні інтенсивності розвитку явищ, які відображаються двома динамічними рядами, обчис­люють коефіцієнт випередження. Він являє собою відношення базисних темпів зростання двох диламічних рядів за однакові проміжки часу:

К_вип=

Якщо швидкість процесу в межах періоду, який вивчають, не однакова, то визначають прискорення чи уповільнення зростання. Якщо інтервали часу одна­кові, можна зіставляти базисні характеристики швид­кості, якщо інтервали часу неоднакові — середні.

Абсолютне прискорення зростання мож­на виявити на основі розрахунків за формулою

воно характеризується додатною величиною > О, уповільнення — від'ємною < 0.

Коефіцієнт прискорення (уповільнення) від­носної швидкості динаміки має вигляд

K_t=

Абсолютне значення одного відсотка приросту - це відношення абсолютного приросту до темпу приросту

A%₌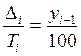

де А% - абсолютне значення одного відсотка при­росту; T_i— ланцюговий темп приросту; y_i-1 - рівень ряду, попередній відносно у_i.

Розглянемо на прикладі застосування цих показників.

Приклад 6.1

Маємо дані про введення в дію загальної площі житлових будинків в Україні за 1990-1994 роки

-(табл.6.1):

Рік
Площа, млн кв.м.	17,4	14,5	14.1	12,3	10,1

 

Визначіть вид ряду динаміки. На основі обчисле­них характеристик ряду динаміки зробіть висновки про тенденцію. Розрахуйте за період 1990-1994 pp. се-редню введену площу житлових будинків за рік, се­редньорічні темпи зростання (падіння) введеної пло­щі.

Маємо інтервальний ряд динаміки з рівними інтервалами. Середній рівень розраховується за фор­мулою середньої арифметичної простої

=13,68 млн кв.м.

Для подальших розрахунків побудуємо табл. 6.2.

Таблиця 6.2

Розрахунок показників динамікиТемпи приросту за 1990-1994 роки (базисні):

Рік	Площа млн. кв.м	Абсолютний приріст млн. кв.м	Темп росту	Темп приросту%	Абсолютне значення одного відсотка приросту, Площа млн. кв.м
ланцюговий	базисний	ланцюговий	базисний	ланцюговий	базисний
	17,4	-	-	1,00	1,00	-	-	-
	14,5	-2,9	-2,9	0,83	0,83	-17	-17	0,174
	14,1	-0,4	-3,3	0,97	0,81	-3	-19	0,145
	12,3	-1,8	-5,1	0,87	0,71	-13	-29	0,141
	10,1	-2,2	-7,3	0,82	0,58	-18	-42	0,123
разом	68,4	-7,3	*	0,58	*	*	*	*

 

Абсолютні прирости за 1900-1994 роки (ланцюгові):

_(1991/1990)=14,5-17,4=-2,9 млн. кв.м;

_(1992/1991)=14,1-14,5=-0,4 млн. кв.м;

_(1993/1992)=12,3-14,1=-1,8 млн. кв.м;

_(1994/1993)=10,1-12,3=-2,2 млн. кв.м;

Абсолютні прирости за 1990-1994 роки (базисні):

_(1991/1990)=14,5-17,4=-2,9 млн. кв.м;

_(1992/1990)=14,1-17,4=--3,3млн. кв.м;

_(1993/1990)=12,3-17,4=-5,1 млн. кв.м;

_(1994/1990)=10,1-17,4=-7,3 млн. кв.м;

Темпи росту за 1990-1994 роки (ланцюгові)

_(1991/1990)=14,5/17,4=0,83 кв.м;

_(1992/1991)=14,1/14,5=0,97. кв.м;

_(1993/1992)=12,3/4,1=0,87. кв.м;

_(1994/1993)=10,1/2,3=0,82. кв.м.

Темпи росту за 1990-1994 роки (базисні):

_(1991/1990)=14,5/17,4=0,83 кв.м;

_(1992/1990=14,1/17,4=0,81. кв.м;

_(1993/1990=12,3/17,4=0,71. кв.м;

_(1994/1990) =0,1/17,4=0,58. кв.м.

Темпи приросту за 1990-1994 роки (ланцюгові)

T _(1991/1990)= (0,83-1)-100% = -17%;

T _(1992/І991) = (0,97-1) • 100% = -3%;

T _(1993/1992)= (0,87-1) • 100% = -13%;

T_(1994/1993) = (0,82-1) • 100% = -18%.

Темпи приросту за 1990-1994 роки (базисні)

T _(1991/1990)= (0,83-1)-100% = -17%;

T _(1992/І990) = (0,81-1) • 100% = -19%;

T _(1993/1990)= (0,71-1) • 100% = -29%;

T_(1994/1990) = (0,58-1) • 100% = -42%.

Абсолютне значення одного відсотка приросту:

A%_(1991/1990)= 17,4/100 = 0,174%;

A%_(1992/І991) =14,5/100 = 0,145%;

A% _(1993/1992)= 14,1/100 = 0,141%;

A% _(1994/1993) ⁼ 12,3/10.0-= 0,123%.

Середньорічний абсолютний приріст розраховуєть­ся, виходячи з кінцевого базисного абсолютного при­росту:

-1,825 млн кв. м.

Середньорічний темп зростання знайдемо також, виходячи з кінцевого базисного темпу росту:

 

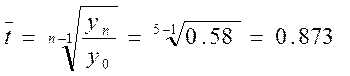
Це означає, що за період з 1990 по 1994 рік вве­дення в дію загальної площі житлових будинків в Ук­раїні знижувалось кожного року в середньому на 12,7%. Порівняльний аналіз ланцюгових темпів зро­стання дає можливість зробити висновок про приско­рення щорічних темпів падіння введення в дію за­гальної житлової площі.

Емпіричні рівні рядів динаміки змінюються внас­лідок дії різних факторів. Характер їх коливання не­однаковий. Проте можна виділити найбільш харак­терні риси, наприклад тендеції розвитку або сезонні коливання, і за допомогою статистичних методів кількісно їх виміряти.