Визначення тенденції розвитку

Тенденція (тренд) - напрям розвитку певного явища. В одних випадках тенденцію можна встано­вити за значеннями рівнів ряду. Розглянемо графічне зображення основних тенденцій.

Рівномірне зростання або зниження представлене на рис. 6.1, уповільнене зростання (зниження) - на рис. 6.2, прискорене зростання (зниження) — на рис. 6.3.

Рис. 6.1. Графік рівномірного зростання (—), зниження (-----).

Рис. 6.2. Графік уповільненого зростання (----), зниження (—).

Рис. 6.3. Графік прискореного зростання (—) та зниження (---).

Якщо ж під впливом випадкових факторів рівні ря­ду не виявляють чіткої тенденції розвитку, то для її виявлення (описування) застосовують спеціальні ста­тистичні засоби.

До найбільш простих методів згладжування ряду відносяться методи ступінчастих середніх та плинних середніх. Обчислення ступінчастих середніх проводиться по збільшеним інтервалам часу. При цьо­му первинні, емпіричні рівні замінюються середніми рівнями. Якщо в динамічному ряді спостерігаються періодичні коливання, то збільшений інтервал слід брати рівним періоду коливання. Такий інтервал «згладжує» випадкові коливання, але не відображає зміну рівнів всередині збільшеного інтервалу.

Суть методу плинної середньої полягає в тому, що середні обчислюються по збільшеним інтервалам при послідовному переміщенні меж інтервалів на один інтервал. При цьому коливання динамічного ряду згладжуються, але недоліком методу є те, що згладже­ний ряд коротше емпіричного, крім того, він лише ілюструє тенденцію, але не дає можливості кількісно ЇЇ виміряти.

Виявити тенденцію та кількісно її виміряти дає змогу метод аналітичного вирівнювання. При цьому

застосовуються «трендові криві» — математичні функ­ції, за допомогою яких описується основна тенденція. Тип функції залежить від специфіки процесу, характе­ру його динаміки: рівномірне, прискорене чи упо­вільнене зростання або зменшення рівнів ряду.

На практиці перевага віддається функціям, пара­метри яких мають чіткий економічний зміст і означа­ють абсолютну чи відносну швидкість розвитку, а са­ме:

• лінійній функції

У_t =a₀+a₁t

де параметр а, характеризує стабільну абсолютну швидкість;

• параболі 2-го ступеня

Y₁=a₀ + a₁t + a₂t²,

яка характеризує стабільний приріст абсолютної швидкості;

• показниковій функції

y_t= a₀a

В усіх функціях t — порядковий номер періоду, а₀ — початковий рівень ряду. Зміст інших параметрів зале­жить від виду функції. Зокрема, а₁ для лінійної — се­редньорічний абсолютний приріст, для показникової - середньорічний темп зростання, для параболи 2-го порядку — початковий абсолютний приріст.

Розглянемо приклад згладжування ряду динаміки (табл. 6.3).

Проведемо згладження ряду методом плинної се­редньої. Середня для перших рівней ряду

 

y₁=

 

Віднесемо його до лютого. Потім залишивши пер­ший рівень (січень) і додавши четвертий (квітень), розрахуємо середню

y₂ = =125 тис. грош. од.

Цим показником замінимо рівень березня. Ру­хаючись таким чином до кінця ряду, розраховуємо усі середні рівні ряду.

Таблиця 6.3

Випуск продукції підприємством по місяцях, тис. грош. од.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Місяць	Випуск продукції
фактичний:	Згладжений методом
плинної середньої	ступінчастих середніх
Січень		-
Лютий
Березень
Квітень
Травень
Червень
Липень
Серпень
Вересень
Жовтень
Листопад
Грудень		-

 

Використовуючи метод ступінчастих середніх, роз­раховуємо спочатку обсяг випуску продукції за три місяці, а потім знайдемо середньомісячний обсяг:

y₁= = 125 тис. грош. од.

y₂= = І29 тис. грош. од.

І так далі (див. табл. 6.3).

Розглядаючи рівні ряду як функцію часу, фактичні рівні ряду замінюють такими, котрі найменш відхи­ляються від фактичних, але мають аналітичний вираз.

Таблиця 6.4

Розрахунки параметрів тренду

 

Місяць	фактичний обсяг,тис.грош.од.	Розрахункові показники
t	t2	yt	Y
Січень		-11		-1298
Лютий		-9		-1116
Березень		-7		-868
Квітень		-5		-640
Травень		-3		-381
Червень		-1		-132
Липень
Серпень
Вересень
Жовтень
Листопад
Грудень
разом					-

 

Для нашого прикладу проведемо аналітичне вирів­нювання за прямою

y = a₀ + a₁ t,

де а₀, a₁- параметри знаходження прямої. Вони зна­ходяться за методом найменших квадратів:

 

 

Дана система буде простішою, якщо за початок відліку визначити середину ряду. Тоді 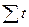= 0 і сис­тема приймає вигляд:

Розв'язок цієї системи є досить простим без вико­ристання методу детермінантів (табл. 6.4).

12a₀= 1581, а₀= 1581/12 = 132 тис. грош. од.

572а₁ = 623, a₁ = 623/572 = 1,089.

За результатами розрахунків рівняння тренду має вигляд:

Y= 132 + 1,089t