При построении группировки с равными интервалами по количественному признаку целесообразно придерживаться следующего алгоритма.
1. Определение оптимального количества групп n.
Число групп n зависит от:
1) задач исследования;
2) группировочного признака;
3) от объема совокупности N;
4) степени вариации группировочного признака.
Оптимальное число групп n определяется подбором или по формуле Стерджесса:
n=1+3,322·lgN,
где N - число единиц совокупности.
Каждая группа должна характеризовать типы явлений, а число единиц в группах должно быть достаточно большим, чтобы можно было делать достаточно обоснованные выводы об исследуемой совокупности.
Когда определено число групп, то следует определить интервалы группировки. Количество групп n и величина интервала h связаны между собой обратной зависимостью.
2. Определение величины интервала группировки: 
где xmax, xmin – соответственно максимальное и минимальное значения признака в совокупности.
Интервал – это: 1) промежуток между максимальным и минимальным значениями признака в группе; 2) значение варьирующего признака, лежащее в определенных границах;
Каждый интервал имеет свою величину, верхнюю и нижнюю границы или хотя бы одну из них. Величина интервала - разность между его верхней и нижней границей. Нижняя граница -наименьшее значение признака в интервале. Верхняя граница - наибольшее значение признака в интервале. Интервал группировок с двумя границами называется закрытым, а с одной верхней или нижней – открытым.
Интервалы группировки в зависимости от их величины бывают равные и неравные.
Равные интервалы применяются при равномерном изменении значений группировочного признака в сравнительно узких границах, а неравные интервалы – при неравномерном изменении в достаточно широких границах.
3. Определение границ каждого интервала 
За нижнюю границу первого интервала 
принимают минимальное значение признака 
, т.е. = Тогда верхняя граница первого интервала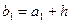 
. Очевидно, что 
. В этом случае нижняя граница второго интервала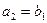 
, верхняя граница второго интервала 
, 
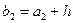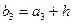и т.д. Замечание. Также за нижнюю границу можно принимать величину 
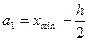, так как 
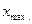и являются случайными величинами и, поэтому, рекомендуется отступить влево от нижней границы .
4. Подсчет числа единиц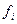 
, попавших в интервал
Для избегания повторного счета единиц, совпадающих с границами интервалов, условимся в каждый интервал включать варианты, равные или большие левой границы и варианты, меньшие правой границы (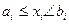
).
Для упрощения расчетов целесообразно построить ранжированный ряд возрастающих значений признака и произвести подсчеты числа единиц в каждой группе. Для автоматического подсчета частот можно использовать редактор MS Excel с помощью статистической функции «Частота» («Вставка - 
Функция – Статистические - Частота»), выделив массивы данных и границ интервалов в соответствующих окнах этой функции.
Замечание. Обычно строят от 7 до 11 групп достаточно заполненных частотами. Если группы не содержат частот, то нужно уменьшить число групп n, тем самым увеличив ширину интервала h.
