Процедура определения параметров объекта при выборе его модели в форме двух- или одноемкостного устойчивого звена с транспортным запаздыванием выполнена в рамках пакета MathCAD. Ниже описаны операции выполняемые в документе, а далее приведены MathCAD документы с выделением областей математических операций и графических объектов.
1. Вначале в документ был введен массив значений разгонной характеристики объекта в виде вектора h, и был сформирован массив значений моментов времени t, соответствующих заданному шагу изменения в 10с.
2. Далее был построен график разгонной характеристики, подобрано «на глаз» значение коэффициента передачи объекта k =0,74, соответствующее асимптотическому поведению функции. Это значение также (для наглядности) наносилось на график в виде пунктирной линии.
3. Затем для объекта управления было составлено (с учетом многоемкостности и наличия эффекта транспортного запаздывания) выражение для передаточной функции 
, которое записывалось согласно формуле (5). После замены аргумента передаточной функции 
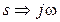была введена формула, связывавшая вещественную часть КЧХ объекта с его переходной функцией 
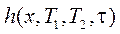[4].
4. Согласно формуле (8) было составлено выражение для целевой функции задачи 
, подлежавшей минимизации путем варьирования своих аргументов. Минимизация проводилась с помощью встроенной функции Minimize пакета MathCAD с предварительным заданием начального приближения.
5. Для проверки точности проведенной процедуры аппроксимации:
вычислялась величина СКО аппроксимирующей функции s от заданных значений в узлах. Достаточно малое значение этой величины (0,0018) доказывало правильность найденных параметров объекта;
визуально оценивалась точность совпадения графика аппроксимирующей зависимости 
с заданными в узлах значениями. Как видно из приведенного графика, заданная и аппроксимирующая зависимости достаточно хорошо совпадают в начальный момент времени, в точке перегиба и в асимптотике. Такое совпадение служит критерием наилучшего приближения.
6. Далее был проведен анализ правильности выбора предельного значения частоты при преобразовании несобственного интеграла (6). Для этого анализировался график ВЧХ объекта U (ω). Как видно из рисунка уже на частоте ω~0,5 c–1 график практически совпадал с осью абсцисс, что является доказательством справедливости нашей замены.
|
Для сравнения приведенный ниже документ отвечает повторению процедуры определения параметров объекта в рамках модели одноемкостного звена с транспортным запаздыванием.
|
