Каждая конечная игра имеет, по крайней мере, одно решение, возможно, в области смешанных стратегий.
Применение оптимальной стратегии позволяет получить выигрыш, равный цене игры: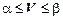 
. Применение игроком А оптимальной стратегии 
обеспечивает ему выигрыш не менее цены игры V, то есть 
.
Применение игроком В оптимальной стратегии 
обеспечивает ему проигрыш, не превышающий цены игры V, то есть
.
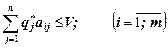Доминирование матричной игры
Доминировать матричную игру, значит, сократить ее размер. Для этого пользуются следующими положениями.
Если в матрице имеются одинаковые (дублирующие) строки, то одна из них оставляется, а другие убираются.
Если в матрице имеются одинаковые (дублирующие) столбцы, то один из них оставляется, а другие убираются.
Если все элементы i – й строки матрицы М меньше или равны соответствующих элементов k – й строки, то i –я стратегия игрока А называется доминирующей и ее следует убрать.
Если все элементы r – го столбца матрицы М больше или равны соответствующих элементов j – го столбца, то для игрока Вr – я стратегия является доминирующей и ее следует убрать.
Игры с природой
На практике часто встречается класс матричных игр, в которых стратегия второго игрока неопределена. Это, так называемые, «игры с природой». Например, нас интересует вопрос об объемах поставок продукции на рынок в условиях полной неопределенности о величине спроса на эту продукцию.
В этом случае выбор стратегии осуществляется на основе критериев, которые позволяют оценить «среднюю прибыль».
Критерий Вальда: 
Критерий Сэвиджа: 
,
где 
- элементы матрицы R – матрицы риска. Эта матрица составляется по правилу: в столбце определяется наибольший элемент и из этого числа вычитаются последовательно все элементы этого столбца.
Критерий Гурвица: 
,
где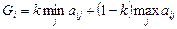 
, значение параметра k 
- задается самим исследователем.
Пример 5. Для заданной матрицы игры
1) Показать существование или отсутствие оптимальных стратегий.
Решение.
Выводы:
, решение в чистых стратегиях; седловая точка 
;
Игрок А выбирает чистую стратегию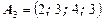 
;
Игрок В выбирает стратегию 
. Цена игры 
.
2) Выполнить доминирование матрицы М.
.
Решение.
1. Элементы 4-го столбца превосходят соответствующие элементы 1-го столбца. Значит, этот столбец доминирующий. Его убираем из матрицы.
2. Во второй матрице доминирующими являются 1-я и 2-я строки, так как их элементы меньше соответствующих элементов 3-й строки. Их убираем.
3. В третьей матрице доминирующими являются 2-й и 3-й столбцы.
4. Получили матрицу, состоящую из одного элемента 
.
Пример 6. Полагая матрицу
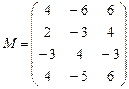
матрицей игры с природой найти решение игры, используя критерии Вальда, Сэвиджа и Гурвица при k = 0,7.
Решение. 1. Критерий Вальда:
.
Вывод: Активные стратегии А2 или А3.
2. Критерий Сэвиджа: Построим сначала матрицу рисков R.
Затем вычислим 
.
Вывод: Активная стратегия А2.
3. Критерий Гурвица (k = 0,7)
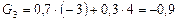
Вывод: Активные стратегии А2 или А3.
Ответ. Рекомендация – выбрать стратегию А2.
СОДЕРЖАНИЕ
| 1. | Цель изучения дисциплины………………………………….. | |
| 2. | Правила и порядок выполнения контрольных работ………. | |
| 3. | Тематический план дисциплины…………………………….. | |
| 4. | Рабочая программа дисциплины…………………………….. | |
| 5. | Список литературы (основная и дополнительная)…………. | |
| 6. | Контрольные вопросы для экзамена за 1 семестр………….. | |
| 7. | Тематика контрольных работ………………………………... | |
| 8. | Контрольная работа №1……………………………………… | |
| 9. | Методические указания по выполнению контрольной работы №1…………………………………………………….. | |
| 10. | Контрольная работа №2……………………………………… | |
| 11. | Методические указания по выполнению контрольной работы №2…………………………………………………….. | |
