Случайное событие, называемое также событием, – это такое явление, которое может либо произойти, либо не произойти в результате испытания.
Классическое определение вероятности. Если множество всех элементарных исходов конечно и все исходы равновозможны, то вероятность события А определяется как
 ,
,
где  – число исходов, благоприятных для А,
– число исходов, благоприятных для А,  –общее число всех возможных элементарных исходов.
–общее число всех возможных элементарных исходов.
Событие, вероятность которого равна 1, называется достоверным, событие, вероятность которого равна нулю, – невозможным. Вероятность события А и противоположного ему события  связаны соотношением
связаны соотношением
 .
.
События называются несовместными, если одновременное их осуществление невозможно, в частности, А и  несовместны.
несовместны.
Для любых событий А и В
 ,
,
для трех событий

Условная вероятность  события А, т.е. вероятность события А, которую находят в предположении, что событие B уже наступило, определяется формулой
события А, т.е. вероятность события А, которую находят в предположении, что событие B уже наступило, определяется формулой

События А и В называются независимыми, если  .
.
Задача 9. В ящике содержится 7 одинаковых, тщательно перемешанных шаров, причем 4 из них – красные, 2 – синие и 1 – белый. Наудачу вынимается один шар. Найдем вероятность того, что вынутый шар а) синий, б) белый, в) цветной.
Решение
Появление синего шара будем рассматривать в качестве события А, появление белого шара – в качестве события В и появление цветного шара – в качестве события С.
Возможны следующие 7 равновозможных исходов испытания (извлечения шара из ящика): В 1 – появился белый шар, В 2, В 3, В 4, B 5 – появился красный шар, В 6, В 7 – появился синий шар, т.е.

Событию А благоприятствуют исходы В 6 и В 7 (два исхода), событию В благоприятствует один исход В 1, а событию С – исходы В 2, В 3, В 4, В 5, В 6, В 7, (шесть исходов). Находим
 ,
,  ,
,  .
.
Задача 10. Бросается игральная кость. Определить:
а) вероятность появления верхней грани с цифрой 4;
б) вероятность того, что выпадет нечетное число очков
Решение
а)Пусть событие А – появление верхней грани с цифрой 4. Кость имеет шесть граней, и при бросании может стать верхней любая из шести граней. Следовательно, число возможных элементарных исходов опыта 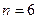 . Из шести граней только одна соответствует цифре 4, поэтому число благоприятных исходов опыта
. Из шести граней только одна соответствует цифре 4, поэтому число благоприятных исходов опыта  . Следовательно, получим:
. Следовательно, получим:
 .
.
б) Пусть событие В – выпадение на верхней грани нечетного числа очков. Число возможных элементарных исходов опыта 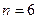 . Только три цифры являются нечетными: 1, 3 и 5, следовательно
. Только три цифры являются нечетными: 1, 3 и 5, следовательно  . Таким образом, получим:
. Таким образом, получим:
 .
.
Ответ: а) вероятность появления верхней грани с цифрой 4 равна  ;
;
б) вероятность того, что выпадет нечетное число очков, равна 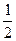 .
.
Задача 11. Отдел технического контроля обнаружил 5 бракованных книг в партии из случайно отобранных 100 книг. Найти относительную частоту появления бракованных книг.
Решение
Относительная частота события А (появления бракованных книг) равна отношению числа испытаний, в которых появилось событие А, к общему числу испытаний:

Ответ: относительная частота появления бракованных книг равна 0,05.
Задача 12. В урне 2 белых, 3 красных и 5 синих одинаковых по размеру шаров. Какова вероятность, что шар, наугад вынутый из урны (без возращения), будет красным или синим?
Решение
Пусть событие А – извлечение из урны красного шара; событие В – извлечение из урны синего шара. Тогда событие  – извлечение из урны красного или синего шара. События А и В – несовместны, поэтому
– извлечение из урны красного или синего шара. События А и В – несовместны, поэтому  Имеем:
Имеем:

Тогда  .
.
Ответ: вероятность, что шар, наугад вынутый из урны (без возращения), будет красным или синим, равна 0,8.
Схема независимых испытаний (схема Бернулли). Проводится  независимых испытаний, в каждом из которых может произойти один из двух исходов: успех или неуспех. Вероятность успеха в каждом из этих испытаний постоянна и равна
независимых испытаний, в каждом из которых может произойти один из двух исходов: успех или неуспех. Вероятность успеха в каждом из этих испытаний постоянна и равна  . Вероятность неуспеха в одном испытании равна
. Вероятность неуспеха в одном испытании равна  .
.
Вероятность того, что в  испытаниях будет ровно т успехов, дается формулой Бернулли:
испытаниях будет ровно т успехов, дается формулой Бернулли:
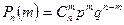 ,
,
где 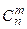 – число сочетаний из n по m.
– число сочетаний из n по m.
Пусть задано множество, состоящее из  элементов. Каждое его неупорядоченное подмножество, содержащее
элементов. Каждое его неупорядоченное подмножество, содержащее 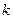 элементов, называется сочетанием из
элементов, называется сочетанием из  элементов по
элементов по  элементов.
элементов.
Число всех сочетаний из  элементов по
элементов по  элементов обозначается
элементов обозначается  («С (це) из
(«С (це) из  по
по 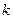 ). Для числа сочетаний справедлива формула:
). Для числа сочетаний справедлива формула:
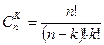
В указанной формуле произведение всех натуральных чисел от 1 до  обозначается
обозначается  ! («
! (« (эн) факториал), т.е.
(эн) факториал), т.е.  !=
!=  .
.
Задача 13. Два равносильных шахматиста играют в шахматы. Что вероятнее: выиграть две партии из четырех или три партии из шести (ничьи во внимание не принимаются)?
Решение
Играют равносильные шахматисты, поэтому вероятность выигрыша  ; следовательно, вероятность проигрыша
; следовательно, вероятность проигрыша  . Так как во всех партиях вероятность выигрыша постоянна и безразлично, в какой последовательности будут выигрываться партии, то применима формула Бернулли.
. Так как во всех партиях вероятность выигрыша постоянна и безразлично, в какой последовательности будут выигрываться партии, то применима формула Бернулли.
Найдем вероятность того, что две партии из четырех будут выиграны:
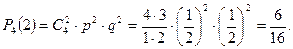
Найдем вероятность того, что три партии из шести:

Так как 
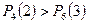 , то вероятнее выиграть две партии из четырех, чем три из шести.
, то вероятнее выиграть две партии из четырех, чем три из шести.
Ответ: вероятнее выиграть две партии из четырех, чем три из шести.
Задача 14. В семье пять детей. Найти вероятность того, что среди этих детей: а) два мальчика; б) не более двух мальчиков; в) не менее двух и не более трех мальчиков. Вероятность рождения мальчика принять равной 0,51.
Решение
По условию вероятность рождения мальчика  , тогда вероятность противоположного события (вероятность рождения девочки)
, тогда вероятность противоположного события (вероятность рождения девочки)  . Для нахождения искомых вероятностей применим формулу Бернулли:
. Для нахождения искомых вероятностей применим формулу Бернулли:
а) вероятность того, что среди пяти детей два мальчика, равна:

б) вероятность того, что среди этих детей не более двух мальчиков (в семье нет мальчиков или в семье один мальчик или в семье два мальчика), равна:
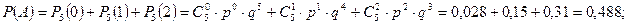
в) вероятность того, что среди пятерых детей не менее одного и не более трех мальчиков (в семье один мальчик или в семье два мальчика или в семье три мальчика), равна:

Ответ: вероятность того, что среди этих детей: а) два мальчика равна 0,31 б) не более двух мальчиков равна 0,488; в) не менее двух и не более трех мальчиков равна 0,71.
Случайные величины
Случайной величиной называется величина, которая в результате испытания принимает одной возможное числовое значение. Случайные величины (с.в.) обозначаются заглавными латинскими буквами.
Дискретная случайная величина имеет конечное или счетное множество значений. Закон распределения дискретное с.в. Х – это перечень ее возможных значений и соответствующих вероятностей. Закон распределения дискретной с.в. Х записывается в виде ряда распределения:
| Значения (х) | 
| 
| … | 
| … | (1) |
| Вероятности (р) | 
| 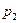
| … | 
| … |
Здесь 
 .
.
Непрерывная с.в. принимает любые значения некоторого (возможно, бесконечного) интервала.
Функция распределения с.в. Х – это функция, определенная равенством:
 .
.
Свойства функции распределения:
1) 
2)  – неубывающая функция;
– неубывающая функция;
3) 
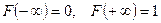 ;
;
4) если все возможные значения случайной величины Х принадлежат интервалу (а,b), то
 при
при 
 при
при 
5)  .
.
Числовые характеристики случайной величины. Математическое ожидание дискретной с.в. определяется формулой:

где  – знак суммирования.
– знак суммирования.
Математическое ожидание обозначается также буквой  , возможно с индексом, например
, возможно с индексом, например  .
.
Перечислим свойства математического ожидания.
- Математическое ожидание константы равно этой константе: МС=С.
- Если С – константа, то М(СХ)=СМХ.
- Математическое ожидание суммы случайных величин равно сумме математических ожиданий.
- Если с.в.
 , независимы, то математическое ожидание их произведения равно произведению математических ожиданий.
, независимы, то математическое ожидание их произведения равно произведению математических ожиданий.
Дисперсия дискретной с.в. Х, имеющей закон распределения (1) и математическое ожидание  , определяется формулой:
, определяется формулой:
 .
.
Дисперсия обозначается также  , возможно, с индексом. Можно также доказать, что
, возможно, с индексом. Можно также доказать, что

Последняя формула иногда бывает удобней для вычислений.
Перечислим свойства дисперсии.
1. Дисперсия постоянной величины равна нулю.
2. Если С – константа, то  .
.
3. Дисперсия суммы (разности) независимых случайных величин равна сумме дисперсий слагаемых:
 .
.
Средним квадратическим отклонением случайной величины Х называется величина  .
.
Задача 15. Дано распределение дискретной случайной величины Х:
| x i | |||||
| p i | 0,1 | 0,2 | 0,1 | 0,3 | 0,3 |
Найти функцию распределения  .
.
Решение
Если  , то
, то  ;
;
если  , то
, то  ;
;
если  , то
, то  ;
;
если 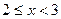 , то
, то  ;
;
если 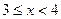 , то
, то 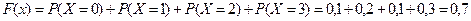 ;
;
если  , то
, то 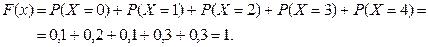
Итак, искомая функция распределения имеет вид:

График полученной функции представлен на рис. 1.

Рис. 1.
Задача 16. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение дискретной случайной величины Х, заданной следующим законом распределения:
| x i | -2 | |||
| p i | 0,5 | 0,1 | 0,2 | 0,2 |
Решение
Вычислим математическое ожидание дискретной случайной величины Х:
 .
.
Далее вычислим дисперсию дискретной случайной величины Х:
 ,
,
а также среднее квадратическое отклонение:
 .
.
Ответ: MX = –0,4; DX = 2,84; σX = 1,65.
Нормальное распределение. Еслиплотность распределения непрерывной случайности величины X равна
 ,
,
то говорят, что с.в. X имеет нормальное распределение; 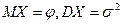 . Если X имеет нормальное распределение с математическим ожиданием µ и средним квадратическим отклонением
. Если X имеет нормальное распределение с математическим ожиданием µ и средним квадратическим отклонением  , то вероятности, связанные с X, вычисляются по формулам
, то вероятности, связанные с X, вычисляются по формулам
 ,
,
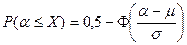 ,
,
 ,
,
где Ф(x) – функция Лапласа; значения функции Лапласа приведены в таблице Приложения 1.
Задача 17. Математическое ожидание и среднее квадратическое отклонение нормально распределенной случайной величины Х соответственно равны 10 и 2. Написать плотность распределения вероятностей и найти вероятность того, что Х примет значение из интервала (12; 14).
Решение
В нашем случае а = 10, σ = 2, так как случайная величина распределена по нормальному закону, то ее плотность находим следующим образом:
 .
.
Вероятность того, что распределенная по нормальному закону случайная величина Х примет значение из интервала (12;14), находится следующим образом:
 .
.
Ответ: 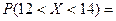
 .
.
Приложение 1
Таблица значений функции 
| Сотые доли | ||||||||||
| х | ||||||||||
| 0,0 0,1 0,2 0,3 0,4 | 0,0000 | |||||||||
| 0,5 0,6 0,7 0,8 0,9 | ||||||||||
| 1,0 1,1 1,2 1,3 1,4 | ||||||||||
| 1,5 1,6 1,7 1,8 1,9 | ||||||||||
| 2,0 2,1 2,2 2,3 2,4 | ||||||||||
| 2,5 2,6 2,7 2,8 2,9 | ||||||||||
| 3,0 3,1 3,2 3,3 3,4 | ||||||||||
| 3,5 3,6 3,7 |
Критерии для оценки контрольной работы:
1. Наличие разумных пояснений к выполняемым пунктам задания
2. Указание используемых формул
3. Соблюдение рекомендованного алгоритма решения задания
4. Точность вычислений
5. Решение всех указанных задач.
Перечень вопросов для подготовки к экзамену Часть 1. Линейная алгебра и аналитическая геометрия
1. Декартовы координаты на плоскости. Координаты двух точек, симметричных относительно а) оси Ox, б) оси Oy, в) начала координат
2. Расстояние между двумя точками
3. Деление отрезка в данном отношении. Координаты середины отрезка
4. Определение линии на плоскости
5. Прямая линия на плоскости. Уравнение прямой с угловым коэффициентом
6. Общее уравнение прямой
7. Угол между прямыми
8. Условия параллельности и перпендикулярности прямых
9. Уравнение прямой, проходящей через заданную точку в заданном направлении
10. Уравнение прямой, проходящей через две заданные точки
11. Уравнение окружности
12. Определители второго порядка
13. Определители третьего порядка и их свойства. Миноры и алгебраические дополнения
14. Методы вычисления определителей третьего порядка
15. Решение систем линейных уравнений по формулам Крамера
16. Матрицы. Основные определения. Сложение и умножение матриц
17. Обратная матрица и ее вычисление
18. Решение системы линейных уравнений с помощью обратной матрицы
19. Векторы. Действия над ними. Скалярное произведение векторов.
20. Условия параллельности и перпендикулярности двух векторов.
21. Общее уравнение плоскости и его исследование.
22. Уравнение плоскости, проходящей через три данные точки.
23. Условия параллельности и перпендикулярности плоскостей.
24. Расстояние от точки до плоскости.
25. Прямая линия в пространстве. Канонические уравнения прямой.
Часть 2. Математический анализ. Элементы теории вероятностей.
1. Основные элементарные функции их свойства и графики.
2. Определение производной функции в точке. Таблица производных.
3. Правила дифференцирования.
4. Производная сложной функции.
5. Промежутки возрастания и убывания функции. Максимум и минимум функции.
6. Наибольшее и наименьшее значения функции на отрезке.
7. Первообразная. Неопределенный интеграл.
8. Свойства неопределённого интеграла.
9. Таблица неопределённых интегралов.
10. Определение и свойства определенного интеграла.
11. Геометрический смысл определенного интеграла.
12. Формула Ньютона–Лейбница.
13. Вычисление площадей плоских фигур с помощью определенного интеграла.
14. Ряды. Необходимый признак сходимости числовых рядов.
15. Дифференциальные уравнения первого порядка.
16. Классическое и статистическое определения вероятности события.
17. Теоремы сложения вероятностей.
18. Теоремы умножения вероятностей.
19. Формула Бернулли.
20. Дискретные случайные величины. Закон распределения.
21. Математическое ожидание и дисперсия дискретной случайной величины.
22. Предмет и задачи математической статистики. Генеральная и выборочная совокупность.
23. Вариационный ряд. Статистическое распределение выборки.
24. Полигон частот. Гистограмма частот.
25. Точечные и интервальные оценки параметров распределения.
Формат и содержание экзамена, критерии оценки. Экзамен проводится в установленное расписанием время по утвержденным билетам. Билет содержит два теоретических вопроса и одно практическое задание. Практическое задание оформляется в письменном виде со всеми необходимыми комментариями по алгоритму решения. На теоретические вопросы студент отвечает устно. Для получения оценки «Отлично» необходимо правильно решить практическое задание, знать основные положения теоретических вопросов и уметь объяснить любую, предложенную преподавателем, задачу из контрольной работы студента. Для получения оценки «Хорошо» необходимо знать основные положения теоретических вопросов и уметь объяснить любую, предложенную преподавателем, задачу из контрольной работы студента. Для получения оценки «Удовлетворительно» необходимо уметь объяснить любую, предложенную преподавателем, задачу из контрольной работы. Перечень рекомендуемой литературы
Основная литература:
1. Солодовников А.С., Бабайцев В.А., Браилов А.В., Шандра И.Г. Математика в экономике (в двух частях) – М.: Финансы и статистика, 2005.
2. Шипачев В.С. Основы высшей математики. – М.: Высшая школа, 2006.
3. Краснов М.А. и др. Вся высшая математика (в шести томах). – М.: Эдиториал УРСС, 2000.
4. Кремер Н.Ш. и др. Высшая математика для экономистов. – М.: ЮНИТИ, 2002.
5. Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Высшая школа, 2006.
Дополнительная литература:
6. Кремер Н.Ш. и др. Практикум по высшей математике для экономистов. – М.: ЮНИТИ, 2002.
7. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. – М: Высшая школа, 2006.
8. Коровина Л.А. Математика (Элементы аналитической геометрии, линейной алгебры и линейного программирования): Методическое пособие по изучению курса и выполнению расчетных работ для студентов, обучающихся по специальности «Туризм». М.: МАТГР, 2007.
9. Коровина Л.А. Математика (дифференциальное и интегральное исчисления). Учебно-методическое пособие по изучению курса и выполнению расчётных работ. М.: МГИИТ,
2010.
10. Дружинина О.В. Теория вероятностей и математическая статистика. Учебное пособие для студентов. М.: МГИИТ, 2013.






