Исследование функций и построение графиков рекомендуется проводить по следующей схеме:
1) Найти область определения функции.
2) Исследовать функцию на непрерывность; найти точки разрыва функции и её односторонние пределы в точках разрыва.
3) Найти точки экстремума функции и определить промежутки монотонности (интервалы возрастания и убывания функции).
4) Найти точки перегиба графика функции и определить интервалы выпуклости и вогнутости графика.
5) Найти асимптоты графика функции.
6) Построить график функции, используя результаты проведённого исследования.
7) Для функции под пунктом а) найти дополнительно наибольшее и наименьшее значения этой функции на отрезке [ a; b].
Задача 4. Исследовать функцию и построить ее график: у =  (х 3 + 9 х2 + 15 х – 9).
(х 3 + 9 х2 + 15 х – 9).
1) Областью определения данной функции являются все действительные значения аргумента х, то есть, D(у): х Î (- µ; + µ), а это значит, что функция непрерывна на всей числовой оси и её график не имеет вертикальных асимптот.
2) Исследуем функцию на экстремум и определим интервалы монотонности. С этой целью найдём её производную и приравняем к нулю:


Решая полученное квадратное уравнение, делаем вывод о том, что функция имеет две критические точки первого рода: 
 Разбиваем этими точками область определения на части, и по изменению знака производной определим промежутки монотонности (интервалы возрастания и убывания функции) и наличие экстремума функции:
Разбиваем этими точками область определения на части, и по изменению знака производной определим промежутки монотонности (интервалы возрастания и убывания функции) и наличие экстремума функции:

| (- µ, - 5) | - 5 | (- 5, - 1) | - 1 | (- 1, + µ) |

| + | - | + | ||

| | max | ¯ | min | |


3) Определим точки перегиба графика функции и интервалы его выпуклости и вогнутости. Для этого найдём вторую производную заданной функции и приравняем её к нулю:



Итак, функция имеет одну критическую точку второго рода  . Разобьём полученной точкой область определения на части, в каждой из которых установим знак второй производной:
. Разобьём полученной точкой область определения на части, в каждой из которых установим знак второй производной:

| (- µ, - 3) | - 3 | (- 3, + µ) |

| - | + | |

| Ç | т. п. | È |
Значение х = - 3 является абсциссой точки перегиба графика функции, а ордината этой точки

4) Выясним наличие у графика заданной функции наклонных асимптот.
Для определения параметров  и
и  уравнения асимптот
уравнения асимптот  воспользуемся формулами
воспользуемся формулами

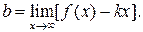
Для заданной функции
 ¥.
¥.
Следовательно, у графика заданной функции наклонных асимптот нет.
5) Для построения графика функции в системе координат хОу изобразим точки максимума А (- 5; 4), минимума В (- 1; - 4), перегиба С (- 3; 0) и точку пересечения графика с осью Оу D (0; - 9 / 4). С учётом результатов исследования построим кривую (см. рис.1).
6) Найдём наибольшее и наименьшее значения функции на отрезке [ - 3; 0 ]. Для этого вычислим значения функции на концах этого отрезка, в критических точках первого рода, попавших на отрезок, и сравним результаты:
у (- 3) = 0; у (- 1) = - 4; у (0) = - 9/4.
Очевидно, что унаиб. (- 3) = 0; унаим. (- 1) = - 4.

Рис. 1
Задача 5. Исследовать функцию и построить ее график: 
1) Область определения функции: D (у) = { хÎ(- µ; 4) È (4; + µ) }.
2) Исследование на непрерывность и классификация точек разрыва.
Заданная функция непрерывна всюду, кроме точки  .
.
Вычислим её односторонние пределы в этой точке:
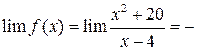 ¥;
¥; 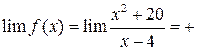 ¥
¥
х®4-0 х®4-0 х®4+0 х®4+0
Таким образом, точка  является для заданной функции точкой разрыва, а прямая
является для заданной функции точкой разрыва, а прямая  - вертикальной асимптотой графика.
- вертикальной асимптотой графика.
3) Исследование на экстремум и промежутки монотонности (интервалы возрастания и убывания функции).
Найдём производную функции, приравняем её к нулю и найдём корни полученного уравнения:






| (-µ; -2) | -2 | (-2; 4) | (4; 10) | (10;+µ) | ||

| + | - | не сущ. | - | + | ||

| | max | ¯ | ¯ | min | |
уmax = у (-2) = - 4; ymin = y (10) = 20.
Обозначим точку максимума А (-2; - 4), точку минимума В (10; 20).
4) Исследование графика на выпуклость, вогнутость и точки перегиба.
Найдём вторую производную функции, приравняем её к нулю и найдём корни полученного уравнения (если они есть).


= 
Так как  ¹ 0, то график заданной функции точек перегиба не имеет. Остаётся выяснить вопрос об интервалах выпуклости и вогнутости графика.
¹ 0, то график заданной функции точек перегиба не имеет. Остаётся выяснить вопрос об интервалах выпуклости и вогнутости графика.

| (- µ; 4) | (4; + µ) | |

| - | не сущ. | + |

| Ç | È |
5) Исследование графика на наличие наклонных асимптот: 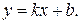



Следовательно, прямая  - наклонная асимптота графика.
- наклонная асимптота графика.
6) Построение графика.
График заданной функции пересекает ось Оу в точке С (0; - 5). Действительно, при  функция
функция 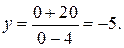
Используя все предыдущие результаты исследования, график заданной функции имеет вид, представленный на рис.2.
При построении графика следует вначале провести асимптоты:  (вертикальная асимптота) и
(вертикальная асимптота) и  (наклонная асимптота); затем нанести точки А (- 2; - 4) - max, В (10; 20) - min и С (0; - 5) - пересечение с осью ОУ; и только потом начертить график.При необходимости можно использовать дополнительные точки.
(наклонная асимптота); затем нанести точки А (- 2; - 4) - max, В (10; 20) - min и С (0; - 5) - пересечение с осью ОУ; и только потом начертить график.При необходимости можно использовать дополнительные точки.

Рис. 2
Таблица основных интегралов
1. 
 8.
8. 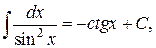
2.  9.
9. 
3.  10.
10. 
4.  11.
11. 
5. 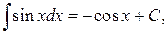 12.
12. 
6.  13.
13. 
7.  14.
14. 
Каждая из формул этой таблицы справедлива в любом промежутке, содержащемся в области определения соответствующей подынтегральной функции.
Справедливость приведённых формул проверяется дифференцированием.
Задача 6. Найти неопределённые интегралы. Проверить результат дифференцированием (в одном из примеров).
а)  б)
б) 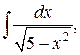
в)  г)
г) 
д)  е)
е) 
Решение.
а) 
= 
б) 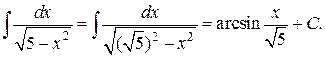
в) 
Нужно использовать формулу интегрирования по частям: 
Для этого обозначим 
 тогда
тогда 

Тогда, применяя формулу интегрирования по частям, получим

г) 


д) 
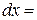

Использована формула:  .
.  е)
е) 

Проверим результат интегрирования в примере д) дифференцированием:

Получили подынтегральную функцию. Следовательно, интеграл нашли верно.
Задача 7. Найти с помощью определённого интеграла площадь плоской фигуры, расположенной в первом квадранте и ограниченной параболой  прямой
прямой  и осью OX (рис.3).
и осью OX (рис.3).
Решение. Сделаем чертёж: в осях ХОУ построим параболу  и прямую
и прямую  и заштрихуем искомую площадь, расположенную в первом квадранте. Затем найдём абсциссу точки пересечения параболы и прямой в первом квадранте. Для этого приравняем правые части уравнений параболы
и заштрихуем искомую площадь, расположенную в первом квадранте. Затем найдём абсциссу точки пересечения параболы и прямой в первом квадранте. Для этого приравняем правые части уравнений параболы  и прямой
и прямой  и решим полученное квадратное уравнение
и решим полученное квадратное уравнение  или
или  Корни этого уравнения
Корни этого уравнения 
 Первому квадранту соответствует корень
Первому квадранту соответствует корень 
Найдём абсциссу точки пересечения прямой  с осью ОХ
с осью ОХ  Решим уравнение
Решим уравнение  , откуда
, откуда 
Искомая площадь фигуры  где
где  площадь фигуры, ограниченной данной параболой
площадь фигуры, ограниченной данной параболой  , вертикальной прямой
, вертикальной прямой  и осью ОХ;
и осью ОХ;  площадь фигуры, ограниченной вертикальной прямой
площадь фигуры, ограниченной вертикальной прямой  данной прямой
данной прямой  и осью ОХ. Вычислим искомые площади:
и осью ОХ. Вычислим искомые площади:
 (кв.ед.)
(кв.ед.)

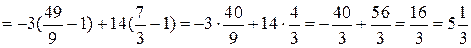 (кв.ед.)
(кв.ед.)
Общая площадь  (кв.ед.)
(кв.ед.)
Задача 8. Найти с помощью определённого интеграла объём тела, образованного вращением вокруг оси ОХ фигуры, расположенной в первом квадранте и ограниченной параболой  прямой
прямой  и осью ОХ (рис.3).
и осью ОХ (рис.3).
Решение. Можно считать, что тело вращения ограничено при  поверхностью, образованной вращением параболы
поверхностью, образованной вращением параболы  вокруг оси ОХ, а при
вокруг оси ОХ, а при  поверхностью, образованной вращением прямой
поверхностью, образованной вращением прямой  вокруг оси ОХ.
вокруг оси ОХ.
Таким образом, общий объём тела вращения будет складываться из двух объёмов:
 Вычислим эти объёмы по формулам:
Вычислим эти объёмы по формулам:
 (куб.ед.)
(куб.ед.)

Для вычисления этого интеграла используем метод замены переменной.
Пусть  Тогда
Тогда  или
или  отсюда
отсюда  Определим новые пределы интегрирования, соответствующие переменной
Определим новые пределы интегрирования, соответствующие переменной  : при
: при 
 а при
а при 

 (куб.ед.)
(куб.ед.)
 (куб.ед.)
(куб.ед.)
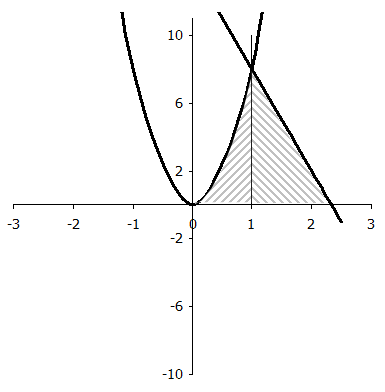
Рис. 3
Ответ: площадь плоской фигуры  (кв. ед.),
(кв. ед.),
объём тела вращения  (куб. ед.)
(куб. ед.)






