| Название контрольной точки | Срок сдачи | Срок проверки |
| Первое задание – выполнить контрольную работу | не позднее 15 января 2014 г. | В течение одной недели после сдачи |
| Второе задание – сдать экзамен | Сессия (февраль 2014 г.) |
Оформленные задания в рукописном виде на листах формата А4 или в тетради в клеточку сдавать на кафедру информационных технологий и математики (к. 208) до указанного срока с записью в журнале контрольных заданий.
Тематический план изучения дисциплины, 1 семестр
| Тема | Виды учебных занятий | |||
| Всего | Ауд. работа | Самостоятельные занятия | ||
| Лекции | Семинар | |||
| Первый семестр Раздел 1. Элементы аналитической геометрии | ||||
| Аналитическая геометрия на плоскости. Метод координат. Расстояние между двумя точками. Деление отрезка в данном отношении. | ||||
| Прямая на плоскости. Угловой коэффициент прямой. Уравнение первой степени. Угол между прямыми. Условия параллельности и перпендикулярности прямых. | ||||
| Раздел 2. Определители. Матрицы. Решение систем линейных уравнений | ||||
| Определители второго и третьего порядка. Их свойства. Миноры и алгебраические дополнения. Методы вычисления определителей. | ||||
| Решение и исследование систем трех линейных уравнений с тремя неизвестными. Формулы Крамера. | ||||
| Матрицы. Действия над матрицами. Обратная матрица и ее вычисление. Решение системы линейных уравнений с помощью обратной матрицы. | ||||
| Раздел 3. Дифференциальное и интегральное исчисление. Элементы теории рядов | ||||
| Производные и дифференциалы функции одной переменной. Геометрический и физический смысл производной. Приложения производной. Максимум и минимум функций. Наибольшее и наименьшее значения функций на отрезке. | ||||
| Интегральное исчисление. Первообразная. Определенный интеграл и его геометрический смысл. Приложения определенного интеграла. Ряды. Необходимый признак сходимости ряда. Дифференциальные уравнения первого порядка. Уравнения в полных дифференциалах. Линейные дифференциальные уравнения второго порядка. | ||||
| Раздел 4. Элементы теории вероятностей, математической статистики и теории массового обслуживания | ||||
| Теория вероятностей. Формулы комбинаторики. Классическое определение вероятности. Теоремы сложения и умножения вероятностей. Схема Бернулли. Случайные величины и их числовые характеристики. | ||||
| Элементы математической статистики. Статистическое распределение выборки. Полигон и гистограмма. Точечные и интервальные оценки параметров распределения. Понятие о статистических критериях. Основы теории массового обслуживания. Входящие потоки. Основные характеристики (длина очереди, периоды занятости, время ожидания). Типы систем обслуживания. Оптимизационные задачи теории массового обслуживания. | Экз.36 | |||
| Всего часов: |
Каждый студент должен решить 8 задач своего варианта. Номер варианта совпадает с последней цифрой учебного номера (шифра) студента. Например, для варианта №6 следует решить задачи №№ 6, 16, 26, 36, 46, 56, 66, 76; для варианта № 0 следует решить задачи №№ 10, 20, 30, 40, 50, 60, 70, 80.
1–10. Даны вершины треугольника АВС.
Найти: 1) длину стороны АВ; 2) уравнения сторон АВ и АС и их угловые коэффициенты; 3) угол А в радианах; 4) уравнение высоты СD и ее длину; 5) уравнение окружности, для которой высота СD есть диаметр; 6) систему линейных неравенств, определяющих треугольник АВС.
1. А (–5; 0), В (7; 9), C (5; –5).
2. A (–7; 2), B (5; 11), С (3; –3).
3. А (–5; –3), В (7; 6), C (5; –8).
4. А (–6; –2), В (6; 7), C (4; –7).
5. А (–8; –4), В (4; 5), C (2; –9).
6. А (0; –1), В (12; 8), С (10; –6).
7. А (–6; 1), В (6; 10), С (4; –4).
8. А (–2; –4), В (10; 5), С (8; –9).
9. А (–3; 0), В (9; 9), С (7; –5).
10. А (–9; –2), В (3; 7), С (1; –7).
11–20. Решить данную систему уравнений с помощью формул Крамера. Сделать проверку полученного решения.
11.  12.
12. 
13.  14.
14. 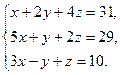
15.  16.
16. 
17.  18.
18. 
19.  20.
20. 
21–30. Систему уравнений записать в матричной форме и решить ее с помощью обратной матрицы. Сделать проверку полученного решения.
21.  22.
22. 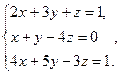
23.  24.
24. 
25.  26.
26. 
27.  28.
28. 
29.  30.
30. 
31-40. Исследовать функцию y = f (x) и построить ее график. Найти наибольшее и наименьшее значения функции y = f (x) на отрезке [ a, b ].
31.  a = - 1, b = 3
a = - 1, b = 3
32. 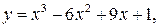 a = - 1, b = 2
a = - 1, b = 2
33.  a = 2, b = 3
a = 2, b = 3
34.  a = - 1, b = 2
a = - 1, b = 2
35.  a = 0, b = 4
a = 0, b = 4
36.  a = - 2, b = 3
a = - 2, b = 3
37.  a = - 3, b = 0
a = - 3, b = 0
38. 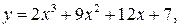 a = -3, b = 1
a = -3, b = 1
39.  a = 1, b = 4
a = 1, b = 4
4 0.  a = - 1, b = 4
a = - 1, b = 4
41-50. Найти с помощью определенного интеграла площадь плоской фигуры, расположенной в первой четверти и ограниченной заданными параболой, прямой и осью Ох.
41. 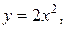

42. 

43. 

44. 

45. 

46. 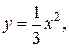

47. 

48. 

49. 

50. 

51–60. В ящике содержится n одинаковых, тщательно перемешанных шаров, причем k из них – красные, l – синие и m – белые. Наудачу вынимается один шар. Найти вероятность того, что вынутый шар а) синий, б) белый, в) цветной.
51. n = 8, k = 3, l = 3, m = 2.
52. n = 9, k = 4, l = 1, m = 4.
53. n = 10, k = 3, l = 5, m = 2.
54. n = 11, k = 5, l = 3, m = 3.
55. n = 12, k = 4, l = 6, m = 2.
56. n = 8, k = 1, l = 5, m = 2.
57. n = 9, k = 3, l = 4, m = 2.
58. n = 10, k = 2, l = 7, m = 1.
59. n = 11, k = 2, l = 4, m = 5.
60. n = 12, k = 3, l = 5, m = 4.
61–70. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение дискретной случайной величины Х, заданной законом распределения.
61.
| xi | ||||
| pi | 0,2 | 0,1 | 0,4 | 0,3 |
62.
| xi | ||||
| pi | 0,5 | 0,1 | 0,3 | 0,1 |
63.
| xi | ||||
| pi | 0,1 | 0,2 | 0,3 | 0,4 |
64.
| xi | ||||
| pi | 0,6 | 0,1 | 0,1 | 0,2 |
65.
| xi | ||||
| pi | 0,3 | 0,2 | 0,1 | 0,4 |
66.
| xi | ||||
| pi | 0,1 | 0,3 | 0,1 | 0,5 |
67.
| xi | ||||
| pi | 0,1 | 0,2 | 0,4 | 0,3 |
68.
| xi | ||||
| pi | 0,2 | 0,1 | 0,4 | 0,3 |
69.
| xi | ||||
| pi | 0,6 | 0,2 | 0,1 | 0,1 |
70.
| xi | ||||
| pi | 0,3 | 0,2 | 0,4 | 0,1 |
71–80. Известны математическое ожидание a и среднеквадратическое отклонение s нормально распределенной случайной величины X. Написать плотность вероятности и найти вероятность попадания этой величины в заданный интервал (a; b).
7 1. a = 11, s = 5, a = 5, b = 10.
72. a = 10, s = 4, a = 6, b = 11.
73. a = 9, s = 1, a = 7, b = 12.
74. a = 8, s = 2, a = 4, b = 10.
75. a = 7, s = 3, a = 4, b = 12.
76. a = 6, s = 5, a = 4, b = 8.
77. a = 5, s = 2, a = 2, b = 7.
78. a = 4, s = 3, a = 1, b = 9.
79. a = 3, s = 2, a = 3, b = 8.
80. a = 2, s = 1, a = 1, b = 4.
Примечание: для контрольной работы следует взять тетрадь в клеточку; представлять рукописный вариант; условия задач переписывать; на титульном листе необходимо указать (можно в напечатанном виде) следующее: МГИИТ, контрольная работа по математике студента ФИО заочного обучения (ускоренная программа обучения), курс, группа, шифр (по зачётной книжке), номер варианта. Проверил: ФИО преподавателя.





