Задача состоит в том, чтобы найти кратчайший путь на графе от какой-то выделенной вершины до любой другой.
Пример: узел 7 – склад, остальные узлы – строительные площадки компании. Показатели на дугах расстояния в километрах.
Надо найти кратчайшие расстояния от склада до каждой строительной площадки. Какова длина кратчайшего пути от склада до строительной площадки 1? Проходит ли кратчайший путь от склада до строительной площадки 1 через строительную площадку 2?
Решим эту задачу методом присвоения меток. Каждому узлу присваиваем метку из двух чисел. Первое число – это минимальное расстояние от узла 7 до данного узла, второе – номер предыдущего узла. Если кратчайшее расстояние от узла 7 определено, то соответствующая метка называется постоянной. Она закрашивается и обозначается круглыми скобками. Все остальные метки – временные, обозначаются квадратными скобками.
Изначально узлу 7 присваиваем метку (0,S), где 0 – расстояние от узла 7 – обозначение стартового узла.
Узел 7 связан с узлами 2,4,6. Длины соответствующих ребер – 17,5,6. Поэтому узлам 2,4,6 присваиваем временные метки -- 
.
Временная метка с наименьшим расстоянием до узла 7 становится постоянной. Это метка (5,7) узла 4. Поэтому следующий шаг начинаем с узла 4.
Узел 4 связан с узлами 2 и 5 без постоянных меток. Длина ребра 4 -- 5 равна 4, метка узла 4 – (5,7) 
временная метка узла 5 равна 
. Длина ребра 4 -- 2 равна 6, метка узла 4 – (5,7) временная метка узла 2 равна 
. Узел 2 помечен меткой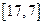 
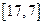, но 11<17 старую метку узла 2 меняем на новую временную метку 
, где 11 – длина пути от узла 7 до узла 2, 4 – номер предшествующего узла.
После этого из всех временных меток 
выбираем метку с наименьшим первым числом. Это 
. Эта метка становится постоянной, а очередной шаг начинаем с узла, соответствующего этой метке, -- узла 6.
Этот узел связан с узлом 5 без постоянной метки. Длина ребра 6-5 равна 2, метка узла 6 – (6,7) временная метка узла 5 равна 
. Но узел 5 уже помечен меткой 
. Так как 8<9, то узлу 5 припишем новую метку 
. После этого из всех временных меток 
метку с наименьшим первым числом 
объявим постоянной, а следующий шаг начнем с соответствующего ей узла 5.
Узел 5 связан только с одним узлом без постоянной метки – узлом 3. Длина ребра 5-3 равна 4, метка узла 5 -- временная метка узла 3 равна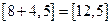 
. Теперь из временных меток 
метку с наименьшим первым числом 
объявляем постоянной, а следующий шаг начнем с соответствующего ей узла 2.
Узел 2 связан с узлами 1 и 3 без постоянных меток. Длина ребра 2-1 равна 15, метка узла 2 -- узлу 1 припишем временную метку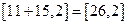 
. Длина ребра 2-3 равна 3, метка узла 2 -- можно пометить узел 3 временной меткой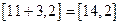 
, но узел 3 уже помечен меткой 
с меньшим первым числом. Поэтому метку 3 не меняем. Теперь из временных меток 
метка с наименьшим первым числом становится постоянной 
, а с соответствующего ей узла 3 начнем следующий шаг. Метку узла 1 меняем на 
. Всем узлам приписаны постоянные метки. Действие алгоритма прекращается.
Первое число метки у каждой вершины – это длина кратчайшего пути от узла 7 до данной вершины. Чтобы восстановить кратчайший путь от узла 7 до какой-то вершины, нужно из этой вершины перейти в соседнюю (ее номер – это второе число метки). И так до вершины 7.
Теперь можно ответить на вопросы задачи. Метка узла 1 -- 
длина кратчайшего пути от узла 7 до узла 1 равна 22. Из узла 1 идем в узел 3. Метка узла 3 -- идем в узел 5. Метка узла 5 -- идем в узел 6. Метка узла 6 -- 
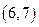
идем в узел 7, т.е. кратчайший путь 1-3-5-6-7. Он не проходит через узел 2.
Задачи.
1. Компания грузовых перевозок осуществляет услуги по перевозке грузов между Воронежем (В) и райцентрами. Так как существенны быстрое обслуживание и минимальные транспортные затраты, то необходим наиболее короткий маршрут. Рисунок отображает сеть дорог. Расстояния указаны в километрах. Найти кратчайшие маршруты от Воронежа до всех 10 райцентров. Какова длина кратчайшего пути от Воронежа до райцентра 10? Проходит ли кратчайший путь от Воронежа до райцентра 9 через райцентр 6?
2. Предложить алгоритм действий при наличии в сети нескольких равных постоянных меток.
