Основные понятия теории графов.
Теория графов представляет собой область дискретной математики, особенностью которой является геометрический подход к изучению объектов и связей между ними. Графы используются при анализе и проектировании сетей электроснабжения, водоснабжения, газоснабжения, теплоснабжения; при анализе и проектировании транспортных сетей, грузовых и пассажирских перевозок и т.д.
Основной объект теории графов – граф – совокупность двух множеств – вершин и ребер.
Пример: схема автодорог, соединяющие населенные пункты Московской области. Множество точек (населенных пунктов) – это множество вершин: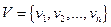 
. Соединяющие линии (автодороги) – множество ребер: 
Два множества в объединении образуют граф: G=(V,X).
Некоторые ребра могут быть изображены в виде стрелок, направленных от начальной вершины к конечной. Их называют дугами. Граф называют ориентированным (орграф), если он содержит дуги. Неориентированный граф состоит только из ребер. Смешанным называют граф, содержащий и ребра и дуги.
Один и тот же граф можно изобразить по-разному. Вершины можно располагать по своему усмотрению и произвольно выбирать форму соединяющих линий. В этом проявляется изоморфизм графов.
Ребро, концевые вершины которого совпадают, называется петлей. Пары вершин графа могут соединяться двумя и более ребрами (дугами одного направления). Такие дуги (ребра) называются кратными. Граф с кратными дугами (ребрами) называется мультиграфом. Изолированная вершина не соединена с другими вершинами.
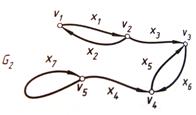
Пример: З адан граф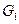 
, состоящий из вершин 
и ребер 
.
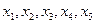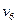-- изолированная вершина, 
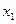и 
-- кратные ребра, 
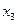-- петля, 
и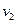 
-- концевые вершины ребра .
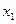Пример: З адан орграф 
. У дуги 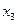вершина 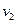-- начальная, а вершина 
-- конечная; 
-- петля.
Маршрут длины m – это последовательность m ребер графа 
(не обязательно различных) таких, что любые два соседних ребра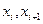 
имеют общую концевую вершину. Замкнутый маршрут приводит в ту же вершину, из которой он начался. Цепь – это маршрут, все ребра которого различны. Простая цепь – это цепь без повторяющихся вершин. Замкнутая цепь называется циклом. Простой цикл – это простая замкнутая цепь.
Пример: Задан граф G.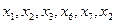 
-- это маршрут длины 6, соединяющий вершины и .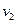
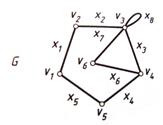
-- замкнутый маршрут длины 7. Он начинается и заканчивается в вершине . 
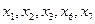-- цепь длины 5 (все ребра в ней различны). Эта цепь не является простой, т.к. при обходе вершину мы посетили два раза. 
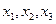-- пример простой цепи (все вершины на нашем пути были различны). 
-- цикл.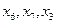 
-- простой цикл.
В случае орграфа вместо слова «цепь» говорят «путь», а слово «цикл» заменяют на слово «контур».
Итак, для задания графа необходимо указать два множества: V – множество вершин и X – множество ребер или дуг. Но при большом числе элементов рисунок графа становится громоздким. В этом случае используют матричный способ.
Различают матрицу смежности и матрицу инцидентности. Если дан граф G с вершинами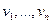 
и ребрами 
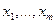, то
Матрица смежности графа G – это квадратная матрица A(G) размерности n x n
(n – число вершин) с элементами
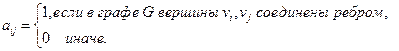
Матрица инцидентности графа G – это матрица В(G) размера n x m (n – число вершин, m – число ребер) с элементами
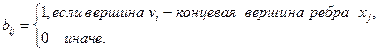
Пример: Для графа G построим матрицу смежности А(G) и матрицу инцидентности В(G).
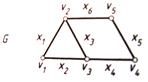
Так как у графа 5 вершин и 6 ребер, то размер матрицы А(G) будет 5x5, а матрицы В(G) – 5x6.
, 
.
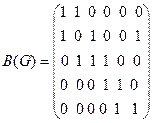Граф G называется связным, если для любых двух его вершин существует маршрут, их соединяющий. Связный граф, не содержащий циклов, называется деревом.
Пример: генеалогический граф (родословное дерево), совокупность всех файлов на дискете.
Граф называется структурным (сетью), если ребра помечены числами. Вершины сети называют узлами, ребра – дугами. Код дерева – последовательность 0 и 1, количество которых в 2 раза больше числа ребер и число нулей равно числу единиц. Начинать обход нужно от корня дерева. По каждому ребру нужно пройти дважды. Первый проход по ребру отмечается 0. Повторный проход – 1. Из всех возможных вариантов выбирается обход по крайнему левому ребру. Заканчивается в корне.
Пример: определим код, соответствующий следующему дереву.
Обозначим ребра дерева буквами латинского алфавита.
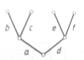
Тогда обход дерева задается следующей последовательностью: a,b,b,c,c,a,d,e,e,f,f,d. По этой последовательности построим код дерева.
Двигаемся по последовательности слева направо. Если буква встречается в последовательности первый раз, то пишем 0, второй – 1. Тогда код равен 001011001011.
По коду дерева можно восстановить само дерево. Двигаемся по последовательности 0 и 1 слева направо. Если очередной символ равен 0, то рисуем новое ребро, если – 1, то двигаемся обратно.
Пример: коду 00011001011101 соответствует следующее дерево.
Задачи
- Определить, какое дерево соответствует коду 0010110011.
