· Выражение вида z=x+iy называется комплексным числом в алгебраической форме. Здесь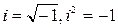 
, x=Re z — действительная (вещественная) часть, а y=Im z — мнимая часть комплексного числа z. Точки, соответствующие действительным числам z=x, расположены на оси OX, а точки, соответствующие мнимым числам z=iy — на оси OY, которую называют мнимой осью комплексной плоскости.
g Изобразим на комплексной плоскости числа 
, 
, 
, 
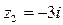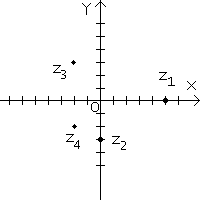
· Число 
называется модулем комплексного числа 
. Угол j, образованный отрезком r (OM) с положительным направлением оси OX называется аргументом комплексного числа z и обозначается 
. Из треугольника OMA: 
, 
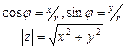, (8)
причем главное значение аргумента j=argz удовлетворяет следующим условиям: 
или 
. Для определенности будем полагать 
.
·Комплексное число 
называется сопряженным числу .
g Найти модуль и аргумент для комплексных чисел, а также записать сопряженное.
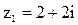
Алгебраическая и тригонометрическая форма записи комплексных чисел. Показательная форма записи комплексных чисел (формула Эйлера).
Подставим в 
выражения (8), тогда получаем 
. (9)
— называется тригонометрической формой комплексного числа z.
По формуле Эйлера 
подставляя в (9) получим формулу
(10)
которая называется показательной формой комплексного числа.
g Запишем число 
в тригонометрической форме. Для этого надо найти модуль и аргумент этого числа. 
Комплексная точка лежит в первой четверти и 
.
Таким образом, в тригонометрической форме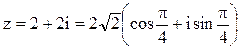 
.
Рассмотрим 
. Для него 
,
| 
|
Главное значение аргумента равно 270°+45°=315°.
.
Самостоятельно найдите тригонометрическую форму чисел 
и 
.
Алгебраические действия с комплексными числами.
Пусть даны два комплексных числа 
и 
.
· Суммой (разностью) двух комплексных чисел называют комплексное число
Например, 
.
· Произведением двух комплексных чисел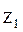 
и 
называется комплексное число 
g Найдите произведение комплексно сопряженных чисел 
, 
· Отношением двух комплексных чисел 
называется комплексное число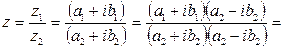 
g Найдите отношение 
на 
· Произведение и отношение комплексных чисел удобно находить в тригонометрической форме. Пусть 
, а 
.Тогда 
,
.
g Выполнить действие над комплексными числами 
, 
, в алгебраической и тригонометрических формах.
, 
, 
.
· Для извлечения корня n-ой степени из комплексного числа в тригонометрической форме используется формула, дающая n значений этого корня:
| (11) |
где 
— арифметический корень из модуля z, а n=0, 1, 2, …, (n-1).
g Вычислить 
.
Решение. Найдем модуль и аргумент данного числа.
, 
;
поскольку x<0, y>0, то число 
находится во второй четверти комплексной плоскости.
, 
, 
По формуле (11)
, k=0, 1, 2.
Отсюда
