Рассмотрим два гармонических колебания, совершаемых телом вдоль координатных осей x и y. При этом частоты этих колебаний одинаковые, амплитуды и фазы различные.
Уравнения колебаний запишутся следующим образом:
х=а·sinwt,
(6)
y=b·sin(wt+j),
где a и b - амплитуды смещений; j - разность фаз обоих колебаний.
Исключив из выражения (6) время t и произведя ряд несложных преобразований, получим уравнение траектории результирующего движения:
х2/а2 +у2/b2–(2ху/аb)·cosj=sin2j (7)
Из аналитической геометрии известно, что уравнение (7) есть уравнение эллипса, оси которого ориентированы относительно осей координат произвольно. Положение эллипса и величина его полуосей зависят от амплитуд а и b и разности фаз j. Рассмотрим некоторые частные случаи:
а) разность фаз равна нулю.
В этом случае уравнение (7) примет вид:
(x/a-y/b)2=0,
Откуда получается уравнение прямой:
y=(b/a)x (8)
Колеблющееся тело перемещается по этой прямой, и расстояние его от начала координат будет изменяться со временем по закону:

Следовательно, результирующее движение является гармоническим колебанием вдоль прямой (8) с частотой w и амплитудой  (рис. 4).
(рис. 4).
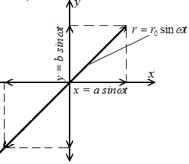
|
| Рис. 4 |
б) разность фаз j=±p/2.
Уравнение (7) переходит в х2/а2+y2/b2=1, т.е. в уравнение эллипса, приведенного к координатным осям. Полуоси эллипса равны соответствующим амплитудам (5). В случае равенства амплитуд а и b эллипс вырождается в окружность. При j=+p/2 телобудет двигаться по эллипсу или окружности по часовой стрелке, а при j=-p/2 - противчасовой стрелки.
Когда разность фаз j имеет произвольное значение, то траектория результирующего движения будет также эллипсом, вписанным в тот же прямоугольник, но с другой ориентацией (рис. 5). В этом случае разность фаз определяется из соотношения sinj=n/m.
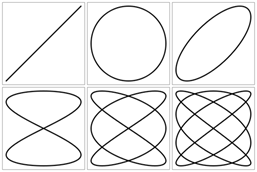
Рис.5
Если частоты взаимно перпендикулярных колебаний не одинаковы, но кратны между собой, например, w1/w2=1/2; 2/3; 3/4 и т.д., то траектория результирующего движения имеет вид довольно сложных кривых, называемых фигурами Лиссажу. Вид этих фигур зависит от отношения частот, от разности начальных фаз, от амплитуд. Фигура Лиссажу при отношении частот 2:3 и разности фаз p/2 показана на рис. 5. Характерным для фигур Лиссажу является то, что если фигуру ограничить координатными осями x и y так, как показано на рис. 5, и подсчитать число касаний фигуры с осью x, равное nx и с осью y, равное ny, то частоты колебаний nх и nу будут связаны соотношением:
n у/nх=nx/ny (9)
Таким образом, если частота одного колебания известна, то частота второго легко определяется по формуле (9).
В данной работе для изучения сложения колебаний используется электронный осциллограф.
Электронный осциллограф предназначен для наблюдения функциональной зависимости величин, преобразованных в электрический сигнал. Наиболее часто осциллографы используют для изучения временной зависимости переменных величин.
Основными частями осциллографа являются электронно-лучевая трубка (ЭЛТ), генератор развертки, блок синхронизации, усилитель вертикального и горизонтального каналов отклонения, блок питания.
Электронно-лучевая трубка является основной частью осциллографа, которая используется для визуализации изображения. Она представляет собой стеклянный баллон, из которого откачен воздух, с находящимися внутри электродами. С одного конца стеклянный баллон имеет расширение, на торцовую часть которого (экран) нанесен слой вещества, светящегося под ударами электронов.
Для получения на экране ЭЛТ устойчивого изображения, необходимо чтобы электронный луч начинал свое повторное движение в одной и той же фазе. Это может быть только в том случае, если период пилообразных колебаний равен или кратен периоду исследуемых колебаний. Процесс согласования фаз называется синхронизацией развертки и осуществляется с помощью блока синхронизации.
Усилители горизонтального и вертикального каналов отклонения позволяют изменять напряжение, подаваемое на горизонтальные и вертикальные пластины ЭЛТ, при этом изображение на экране растягивается или сжимается по соответствующему направлению.
Блок питания обеспечивает подачу необходимых напряжений на ЭЛТ, усилители, генератор развертки и другие узлы осциллографа.
С помощью электронного осциллографа можно измерить амплитуду исследуемого напряжения. Для этого необходимо знать чувствительность осциллографа - отклонение светового пятна при изменении напряжения на отклоняющих пластинах на 1В (измеряется в см/В). Так как имеются две отклоняющие независимые системы: по горизонтальной оси Х и по вертикальной оси У, то соответственно можно указать и две чувствительности S x и Sy:
Sx=X/Ux, Sy=Y/Uy (10)
Используя осциллограф, можно также определить частоту исследуемого сигнала.
ХОД РАБОТЫ
I. Определение чувствительности осциллографа:
а) включите осциллограф в сеть и дайте ему прогреться в течении 2-3 минут;
б) подайте на вход У осциллографа напряжение Uэф с регулятора напряжения, развертку по оси Х отключите;
в) установите длину вертикального отрезка на экране осциллографа, равную L;
г) вычислите амплитудное значение напряжения:

д) рассчитайте чувствительность Sу осциллографа:
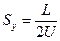 ;
;
е) определите чувствительность осциллографа при двух других значениях подаваемого напряжения и вычислите среднее значение чувствительности;
ж) результаты измерений и вычислений занесите в табл. 1.
Таблица 1.
| № | Uэф, В | U, B | L, мм | Sy, мм/В | ΔSy, мм/В | ɛ, % |
| Ср.знач. |
II. Определение амплитудного значения напряжения:
а) не меняя положения ручек регулировки усиления канала вертикального отклонения, подайте на вход Y осциллографа сигнал с выхода регулятора напряжения (развертка по оси X отключена);
б) измерьте длину L получившегося на экране вертикального отрезка;
в) вычислите амплитудное значение напряжения:

III. Определение частоты сигнала по фигурам Лиссажу:
а) подайте на вход Х осциллографа сигнал с известной частотой νx с регулятора напряжения;
б) на вход Y осциллографа подайте исследуемый сигнал с генератора звуковой частоты с неизвестной частотой νy;
в) получите на экране устойчивое изображение фигуры Лиссажу и зарисуйте его;
г) на зарисованной фигуре провести оси Х и У (в местах, где количество точек пересечения с фигурой будет наибольшим);
д) посчитать количество точек пересечения фигуры с осями: с осью ОХ – nx, с осью ОУ – nу.
е) Зная значения nx и nу определить частоту νy исследуемого сигнала по формуле
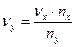
ж) Пункты б-е повторить для трех неизвестных сигналов. Данные занести в таблицу 2.
Таблица 2.
| № | Фигура Лиссажу | νx, Гц | nx | ny | νy, Гц |
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Из каких блоков состоит электронный осциллограф?
2. Что называется чувствительностью осциллографа?
3. Что такое синхронизация сигналов и для чего она нужна в осциллографе?
4. Что такое фигуры Лиссажу и как их получают в данной работе?
5. Для каких целей может быть использован осциллограф?
6. Как с помощью осциллографа можно измерить амплитуду и частоту исследуемого сигнала?
7. Что такое "биения", какова их частота и амплитуда?
Лабораторная работа № 5






