При возрастании скорости и размеров потока (или убывания вязкости) силы инерции становятся, при прочих равных условиях, близкими по величине к силам вязкости. Случайные искривления траекторий частиц жидкости возникают легче и существуют дольше. Этому режиму течения жидкости соответствует некоторая область значений числа Рейнольдса, которая называется критической.
Наконец, если число Рейнольдса больше критического значения, силы инерции значительно превышают силы вязкости и случайно возникшие возмущения развиваются в толще потока. Со временем весь поток оказывается заполненным возмущениями. Частицы жидкости движутся по искривлённым, случайно изменяющимся во времени траекториям. Такое движение называется турбулентным.
Переход от ламинарного к турбулентному режиму течения наблюдается для всех жидкостей при одном и том же значении числа Рейнольдса Reк (критическое значение). Следовательно, критическая скорость vк, при которой осуществляется переход, меняется в зависимости от размеров потока и вязкости таким образом, что критическое значение числа Рейнольдса для всех жидкостей остаётся постоянным.
Ламинарному течению соответствуют значение чисел Рейнольдса, примерно, Re < 1000. Переход от ламинарного к турбулентному течению происходит при значениях числа Рейнольдса 1000 < Re < 2000. При значениях Re > 2000 течение будет турбулентным.
Величина критического значения числа Рейнольдса в заметной степени зависит от характера входа потока жидкости в трубу и от шероховатости её стенок. При гладких стенках и плавном входе в трубу критическое значение Reк может достичь величины 20000. Если входное отверстие не обеспечивает спокойного втекания жидкости в трубу и стенки шероховатые (имеются выступы), то критическое число Рейнольдса может иметь значения: 800 ¸ 1000.
Критическое значение числа Рейнольдса характеризует переход от ламинарного течения к турбулентному не только в случае потока в трубе, но и в любых потоках жидкостей и газов, а также переход от ламинарного обтекания к турбулентному. От числа Рейнольдса зависит величина сопротивления в движущейся жидкости. Равенство чисел Рейнольдса для двух различных потоков является одним из условий их механического подобия, что особенно важно для исследования на моделях течения жидкости в различных условиях (или обтекания различных тел).
В турбулентном потоке частицы жидкости движутся со своими индивидуальными скоростями. Скорости отдельных частиц могут отличаться и по величине, и по направлению. Измеряя скорость в некоторой фиксированной точке пространства, мы обнаружим в ней смену скоростей, так как в данную точку приходят частицы с различными скоростями.
Следовательно, турбулентный поток по существу нестационарен. Однако в случае движения жидкости под действием постоянных сил пульсация скорости происходит около некоторого среднего значения, и оказывается возможным считать такой турбулентный поток в среднем стационарным.
Рассмотрим схему возникновения и развития турбулентности потока. Положим, что жидкость находится в состоянии стационарного течения. При увеличении скорости и достижения критических значений числа Рейнольдса движение потока становится неустойчивым. В нём возникают вихри (на случайных выступах твёрдых стенок, внутри потока вследствие малых колебаний плотности и т.п.). Вихри крупного размера, получающие энергию от основного усреднённого (стационарного) движения, неустойчивы и дробятся на более мелкие вихри вплоть до мельчайших вихрей, которые оказываются уже устойчивыми, т.к. для них число Рейнольдса будет меньше критического. Энергия этих вихрей благодаря вязкости переходит во внутреннюю энергию.
Таким образом, турбулентное движение представляет собой набор (спектр) вихрей различной величины, начиная от крупных (близких по размеру к поперечному сечению потока), и кончая мельчайшими вихрями.
Смена во времени в некоторой точке потока подобных вихрей и создаёт пульсацию скорости. Обычно рассматривают средние скорости в данной точке, полученные как результат усреднения значений скоростей, сменяющих друг друга за время Т.
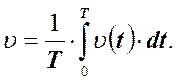(15)
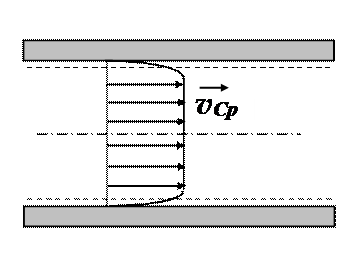В турбулентном потоке распределение средних скоростей имеет вид.
Вблизи твёрдых границ скорость в тонком слое (пограничном слое) резко возрастает до значения, близкого к средней скорости в сечении, а дальше изменяется сравнительно мало. В пограничном слое течение может быть как ламинарным, так и турбулентным в зависимости от скорости течения.
При турбулентном движении сопротивление жидкости оказывается пропорциональным не первой, а второй степени скорости.
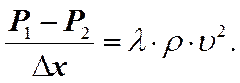(16)
l – коэффициент сопротивления, зависящий от числа Рейнольдса.
Итак, при турбулентном движении: 1) частицы жидкости движутся по случайным хаотически изменяющимся траекториям; 2) их средняя скорость резко возрастает в пограничном слое и почти не меняется вдали от границ потока; 3) сопротивление движению жидкости или твёрдого тела в ней прямо пропорционально второй степени скорости.
